Leetcode 209.长度最小的子数组(画图分析)

力扣传送门(opens new window)

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

• 输入：s = 7, nums = [2,3,1,2,4,3]
• 输出：2
• 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

提示：

• 1 <= target <= 10^9
• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^5

解题思路：

双指针法

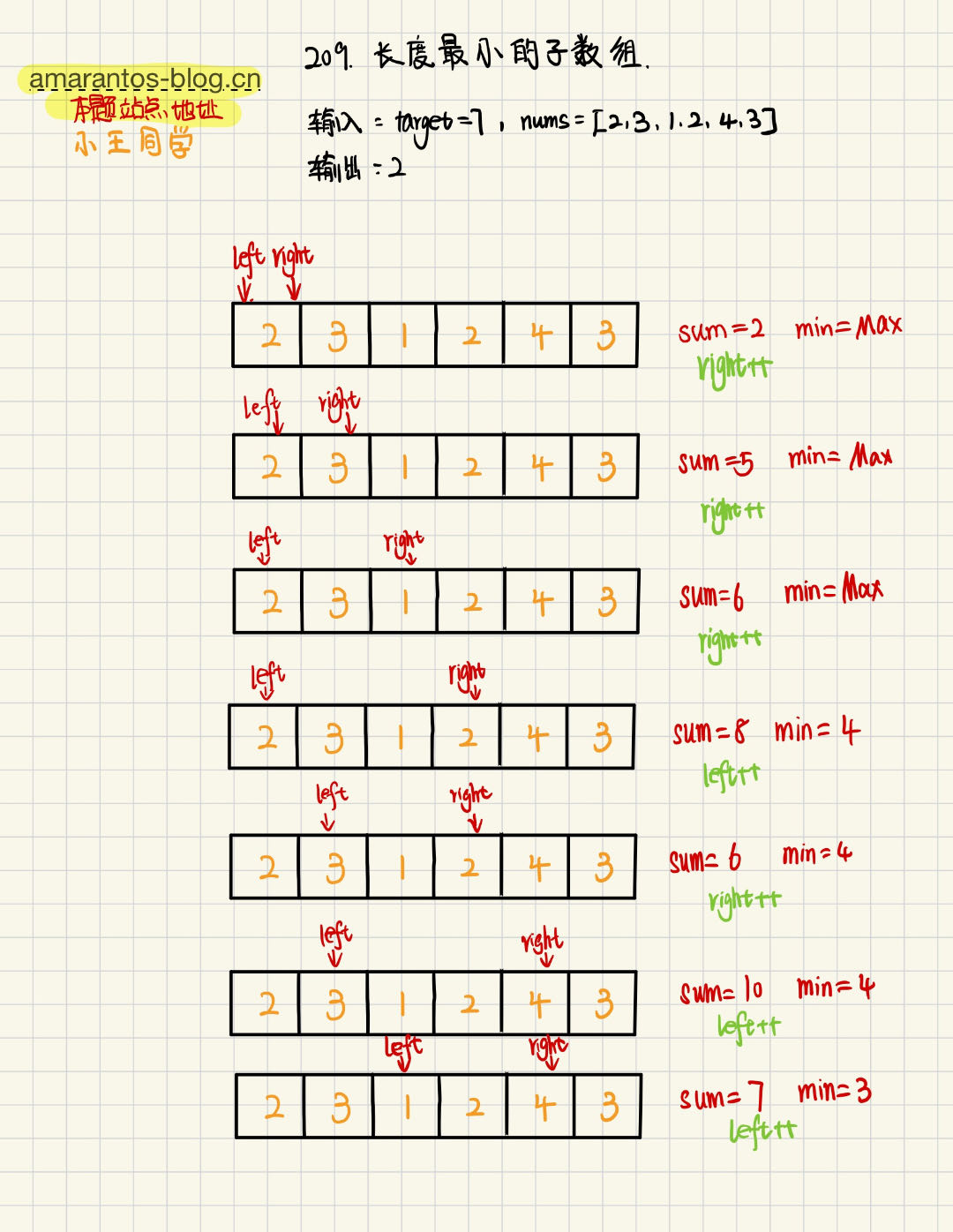
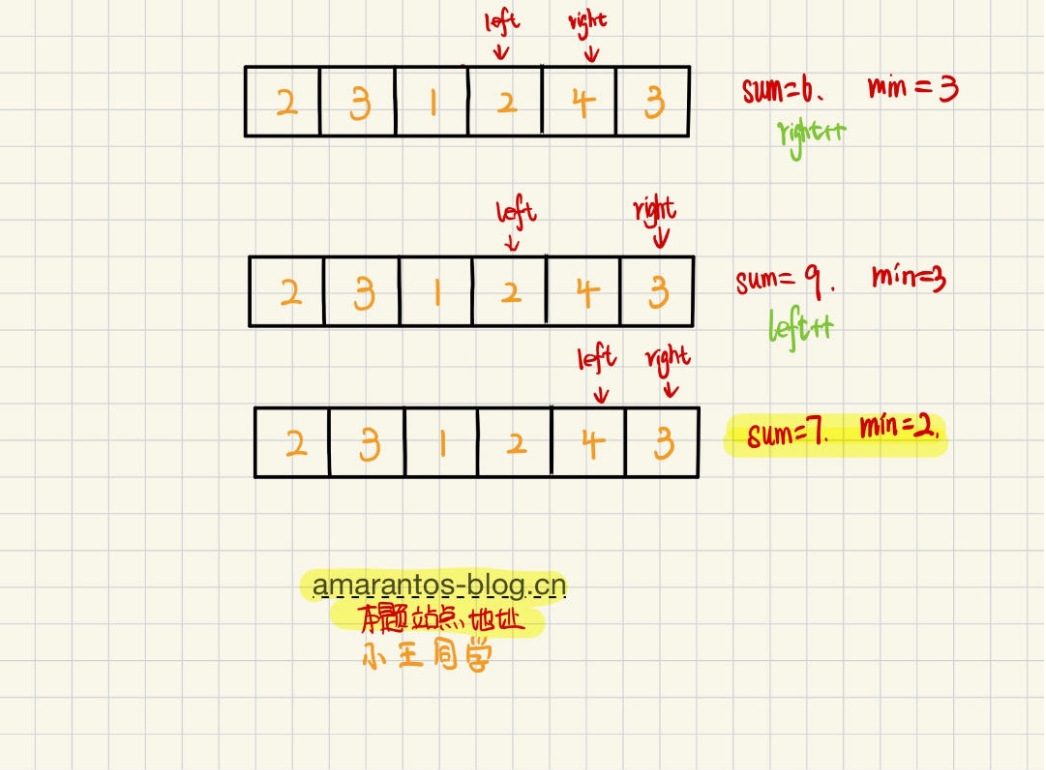
我们使用 left 和 right 两个指针，让 right 和 left 指针都指向第一个节点

只要当前left和right之间的数之和小于 target，right就一直向后移动，直到总和大于等于 target 为止，

接着记录下队列中元素的个数（right - left +1），并且（right - left +1）和我们之前保存的min的值要进行比较取最小的那个。

如果left和right之间的数之和大于 target,再让left指针一直向后移动，直到队列中元素的和小于 s 为止，这个操作目的是尝试找到更短的子数组，期间如果不小于 target，也要记录下队列中元素的个数，这个个数其实就是不小于 target 的连续子数组长度，我们要记录最小的即可。

接着再让right指针向右移动……重复上面的操作，直到right指针走到最后一个元素。

最后求得的最小连续子数组长度 就是答案

具体的可以看我下面画的每一个步骤

代码实现：

java

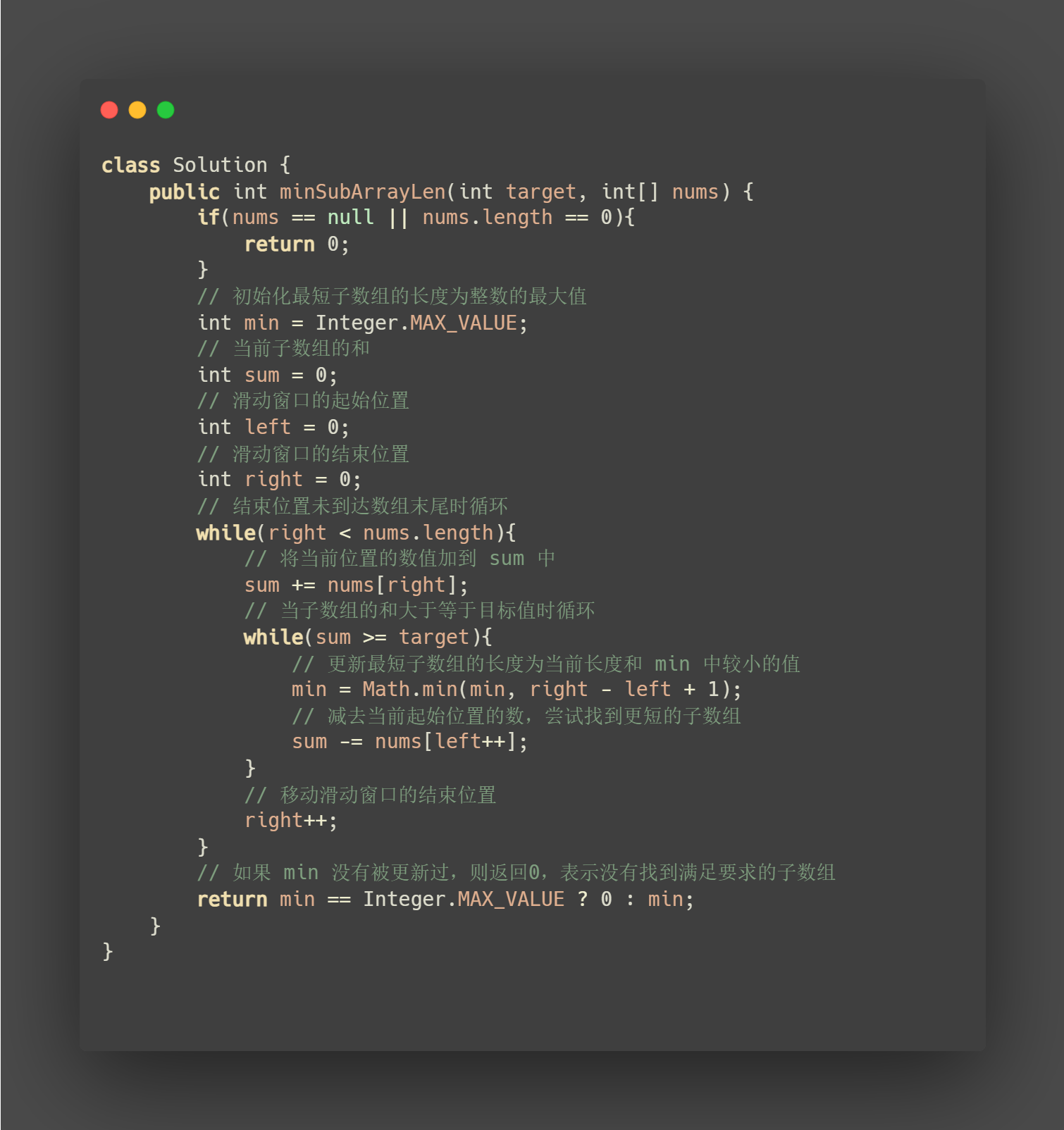
class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        if(nums == null || nums.length == 0){
            return 0;
        }
        // 初始化最短子数组的长度为整数的最大值
        int min = Integer.MAX_VALUE;  
        // 当前子数组的和
        int sum = 0;  
        // 滑动窗口的起始位置
        int left = 0;  
        // 滑动窗口的结束位置
        int right = 0; 
        // 结束位置未到达数组末尾时循环
        while(right < nums.length){  
            // 将当前位置的数值加到 sum 中
            sum += nums[right]; 
            // 当子数组的和大于等于目标值时循环
            while(sum >= target){  
                // 更新最短子数组的长度为当前长度和 min 中较小的值
                min = Math.min(min, right - left + 1);  
                // 减去当前起始位置的数，尝试找到更短的子数组
                sum -= nums[left++];  
            }
            // 移动滑动窗口的结束位置
            right++; 
        }
        // 如果 min 没有被更新过，则返回0，表示没有找到满足要求的子数组
        return min == Integer.MAX_VALUE ? 0 : min;  
    }
}

python3

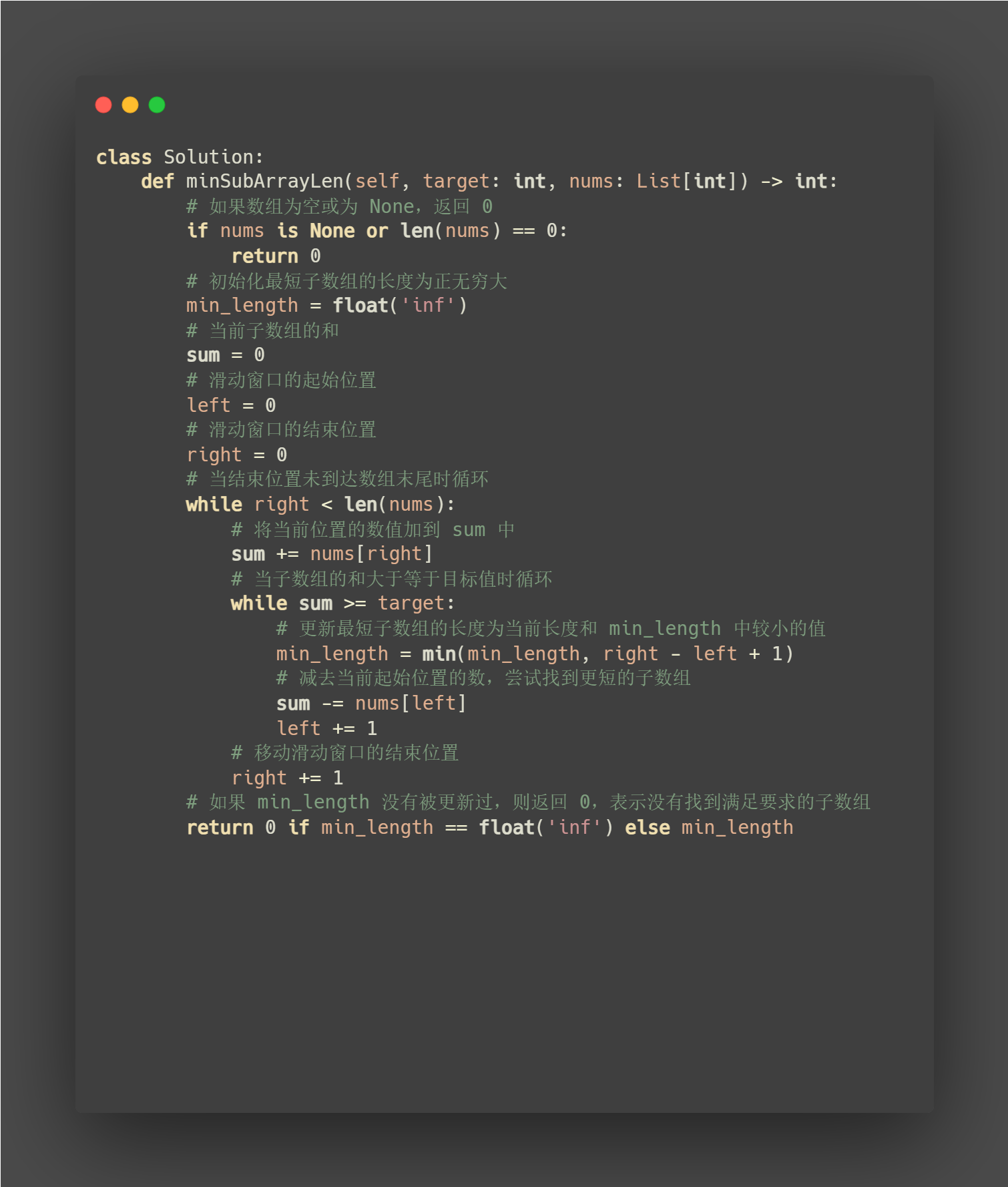
class Solution:
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        # 如果数组为空或为 None，返回 0
        if nums is None or len(nums) == 0:
            return 0
        # 初始化最短子数组的长度为正无穷大
        min_length = float('inf')
        # 当前子数组的和
        sum = 0
        # 滑动窗口的起始位置
        left = 0
        # 滑动窗口的结束位置
        right = 0
        # 当结束位置未到达数组末尾时循环
        while right < len(nums):
            # 将当前位置的数值加到 sum 中
            sum += nums[right]
            # 当子数组的和大于等于目标值时循环
            while sum >= target:
                # 更新最短子数组的长度为当前长度和 min_length 中较小的值
                min_length = min(min_length, right - left + 1)
                # 减去当前起始位置的数，尝试找到更短的子数组
                sum -= nums[left]
                left += 1
            # 移动滑动窗口的结束位置
            right += 1
        # 如果 min_length 没有被更新过，则返回 0，表示没有找到满足要求的子数组
        return 0 if min_length == float('inf') else min_length

c++

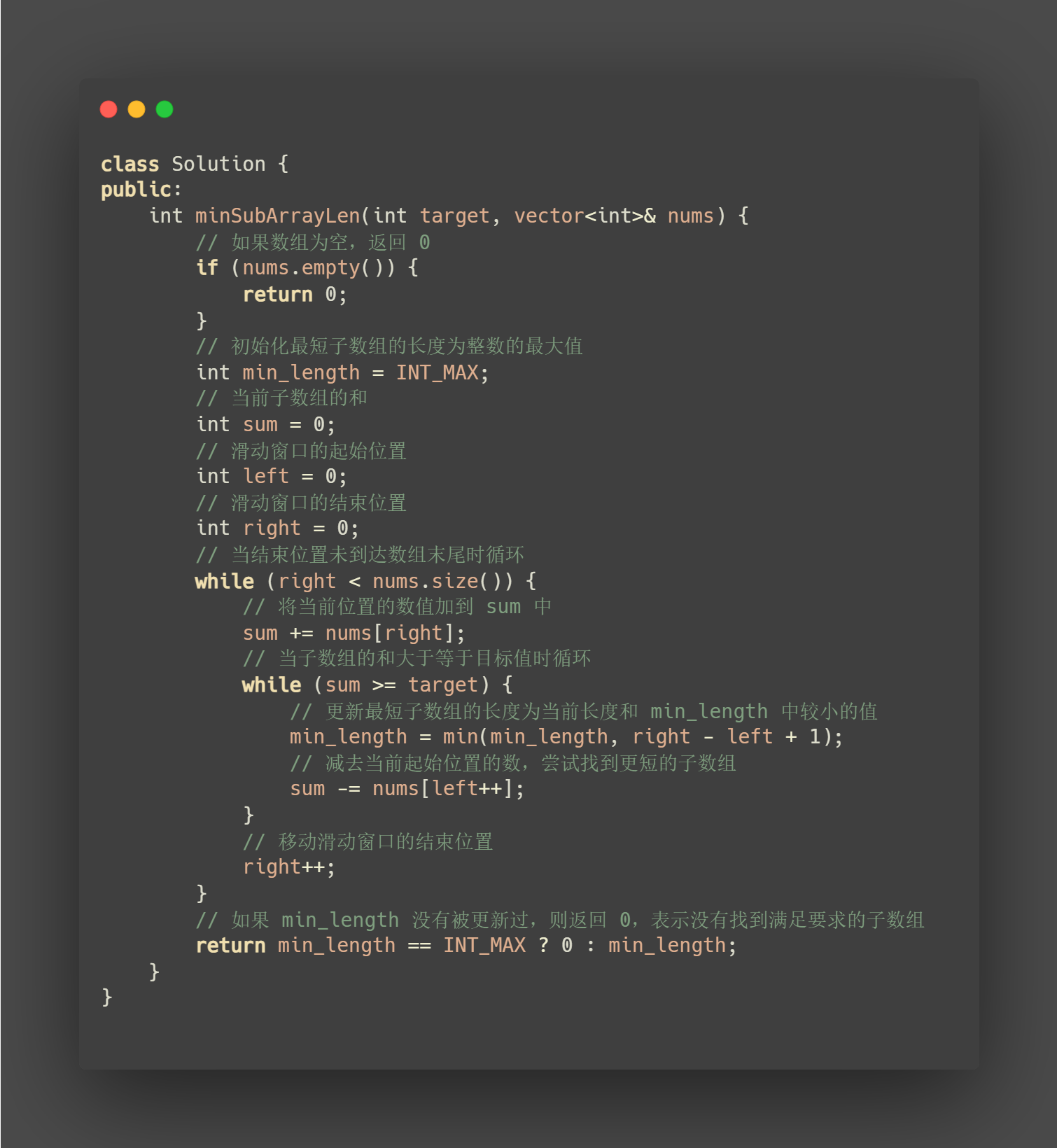
class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        // 如果数组为空，返回 0
        if (nums.empty()) {
            return 0;
        }
        // 初始化最短子数组的长度为整数的最大值
        int min_length = INT_MAX;
        // 当前子数组的和
        int sum = 0;
        // 滑动窗口的起始位置
        int left = 0;
        // 滑动窗口的结束位置
        int right = 0;
        // 当结束位置未到达数组末尾时循环
        while (right < nums.size()) {
            // 将当前位置的数值加到 sum 中
            sum += nums[right];
            // 当子数组的和大于等于目标值时循环
            while (sum >= target) {
                // 更新最短子数组的长度为当前长度和 min_length 中较小的值
                min_length = min(min_length, right - left + 1);
                // 减去当前起始位置的数，尝试找到更短的子数组
                sum -= nums[left++];
            }
            // 移动滑动窗口的结束位置
            right++;
        }
        // 如果 min_length 没有被更新过，则返回 0，表示没有找到满足要求的子数组
        return min_length == INT_MAX ? 0 : min_length;
    }
};