LeetCode-01背包滚动数组理论基础透析（2）

一维滚动数组

上一讲我们讲了01背包的二维数组的解法，这一讲我们对二位数组进行一个优化

使用一维数组进行对空间的优化来实现01背包的问题，也就是滚动数组

还是先看一下题目：

背包最大重量为5。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30
物品3	5	40

问背包能背的物品最大价值是多少？

滚动数组：让数组滚起来。典型的时间去换空间的思路。滚动数组基本上都是在DP和递推中使用，大部分都是通过数组中的值结合其他的数更新数组中的某一位，之后在数组中交换数值的位置，再更新下一位。

不知道大家做动态规划的题有没有理解，始终是初始化数组的前几个元素，一般是已知的，然后根据前面的值去挨个推导后面的元素的值，直到推导出最后一个元素！！！

上一讲的话我们用的二位数组，递推公式为：

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + v[i])

同时我们也知道动态规划中每一个状态都是由上一个状态推导出来的。所以dp[i - 1]可以直接放入到dp[i]。所以可改为：

dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + v[i])

上面的状态转移方程，记录下了每次操作后的最大价值，但是最后需要的结果只有最后一行的最大容量的价值。根据上一行得到下行数据后，上一行的数据就是没有用处的了。所以优化空间，用一个一维数组dp[j]。

这里我刚开始也没理解，为什么可以这样写？？？什么上一层拷贝到当前层，这里我举一个小例子

假设我们有一个整数数组 nums，我们想要计算一个新的数组 dp，其中 dp[i] 表示原数组 nums 中前 i 个元素的累加和。

public class AccumulatedSum {
    public static int[] calculateAccumulatedSum(int[] nums) {
        int n = nums.length;
        int[] dp = new int[n];
        dp[0] = nums[0];

        for (int i = 1; i < n; i++) {
            dp[i] = dp[i] + dp[i - 1];
        }

        return dp;
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3, 4, 5};
        int[] accumulatedSum = calculateAccumulatedSum(nums);

        System.out.println("Accumulated Sum:");
        for (int num : accumulatedSum) {
            System.out.print(num + " ");
        }
    }
}

也就是说上一层循环计算出来的值需要到下一次循环中使用！！！

那我们继续来看，将二维数组 dp[i][j] 转换为一维数组 dp[j] 的方式是基于状态转移方程 dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])，其中 dp[i][j] 表示在考虑前 i 个物品，背包容量为 j 时的最大价值。

让我们来解释为什么可以这样转换。

在背包问题中，每个物品有两个属性：重量 weight[i] 和价值 value[i]。我们要在给定的背包容量 j 下，选择一些物品放入背包，使得放入的物品总重量不超过背包容量，并且总价值最大化。

在二维数组 dp[i][j] 中，i 表示考虑前 i 个物品，j 表示背包容量。状态转移方程 dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + v[i]) 表示，在考虑第 i 个物品时，我们有两种选择：放入第 i 个物品或不放入第 i 个物品。

• 如果我们选择不放入第 i 个物品，则当前状态的最大价值为上一行相同列的值，即 dp[i-1][j]。
• 如果我们选择放入第 i 个物品，则当前状态的最大价值为上一行背包容量减去当前物品重量后的列的值，再加上当前物品的价值，即 dp[i-1][j-weight[i]] + value[i]。

我们需要在这两种选择中取最大值，以获得当前状态的最大价值。

转换为一维数组时，我们可以观察到，对于状态 dp[i][j]，它只依赖于上一行的两个元素 dp[i-1][j] 和 dp[i-1][j-weight[i]]，即当前行的值只与上一行的值有关。因此，我们可以使用一维数组 dp[j] 来存储每一行的值，其中 dp[j] 表示考虑前 i 个物品时，背包容量为 j 时的最大价值。

在状态转移方程 dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + v[i]) 中，将 dp[i][j] 替换为 dp[j]，dp[i][j - weight[i]] 替换为 dp[j - weight[i]]，我们得到转换后的状态转移方程 dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。

因此，可以将二维数组转换为一维数组，并使用一维数组来实现背包问题的动态规划解法。这种转换不仅可以节省空间，还能保持状态转移的正确性。

动态规划解题思路

1. 确定dp数组和其下标的含义
2. 推导出状态转移方程
3. 初始化dp数组
4. 确定遍历的顺序

1. 确定dp数组和其下标的含义

在01背包问题中，dp[j]表示：容量为j的背包，所背的物品价值最大为dp[j]。

2. 推导状态转移方程

• 上一层的 dp[j]即为不放入物品i
• dp[j - weight[i]] + value[i]：容量为j的背包，放入物品i了，减去 weight[i]，加上对应i的价值

依据题意取 dp[j]与 dp[j - weight[i]] + value[i]间较大值。

所以递归公式为:

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

3. 初始化dp数组

因为背包容量为0，所背的物品的最大价值肯定也是0.

4. 确定遍历的顺序

为什么倒叙遍历？？

举个例子：物品0的weight[0] = 1，value[0] = 15
正序遍历：

dp[1] = dp[1 - weight[0]] + value[0] => dp[1] = 15
dp[2] = dp[2 - weight[0]] + value[0] => dp[2] = 30

此时dp[2]就已经是30了，物品0已经被放入了两次，所以不能正序遍历。

倒序遍历：
dp[2] = dp[2 - weight[0]] + value[0] => dp[2] = 15
dp[1] = dp[1 - weight[0]] + value[0] => dp[1] = 15
所以需要从后从后向前遍历，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。另外，如果遍历背包容量放在外层，那么每个dp[j]只会放入一个物品，即背包里只放入了一个物品。所以需要背包容量的遍历要放在内层。

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

手动推导

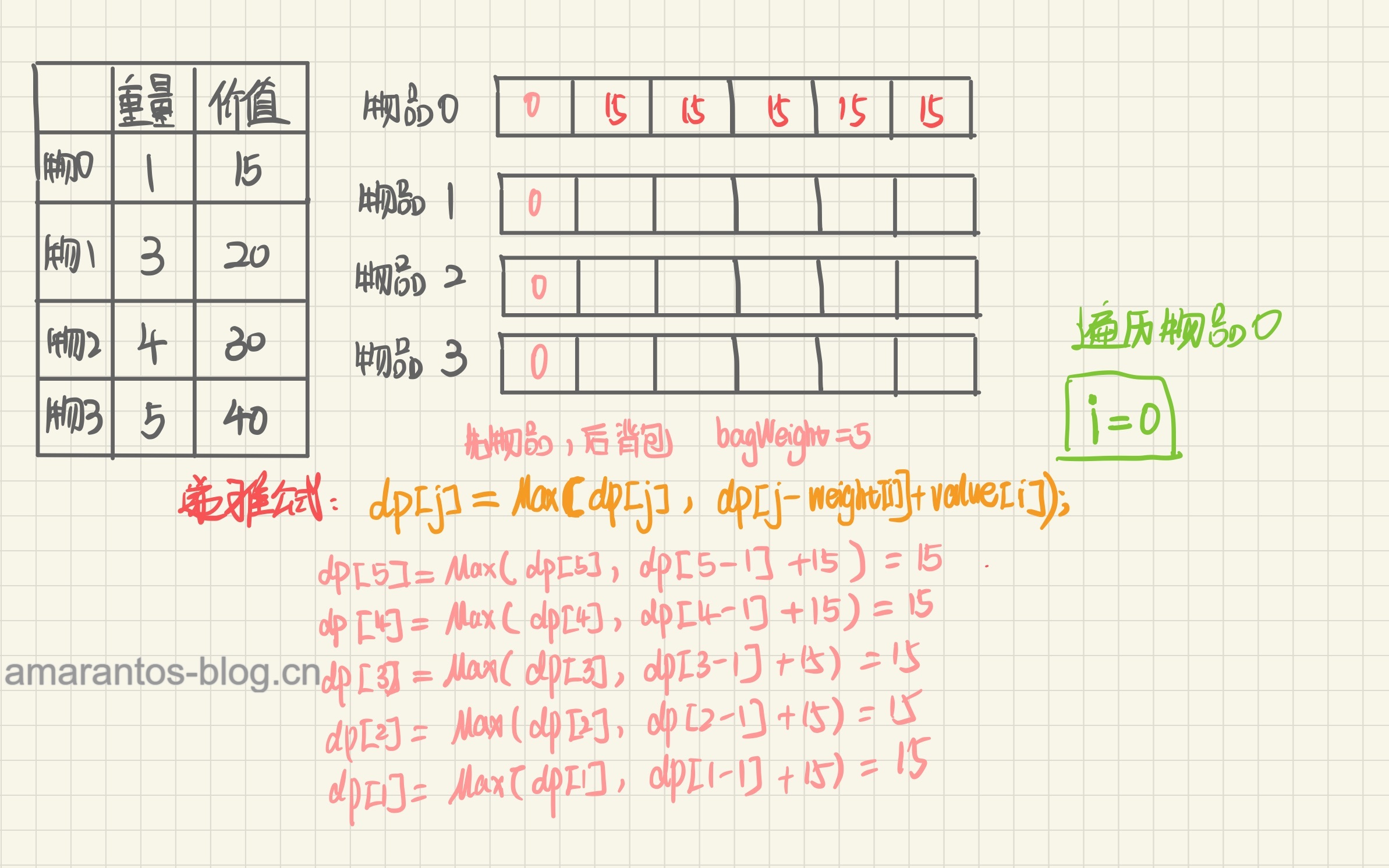
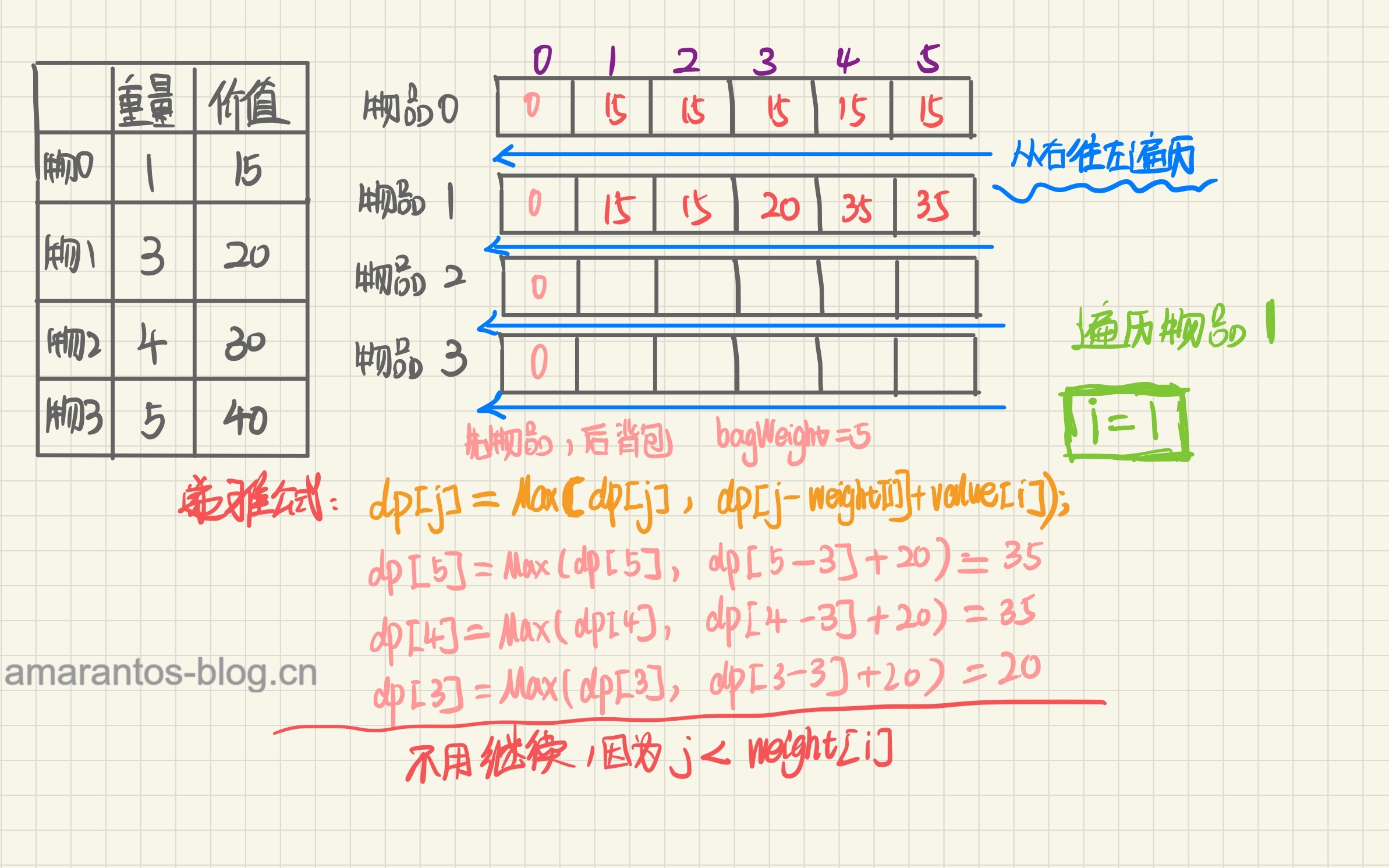
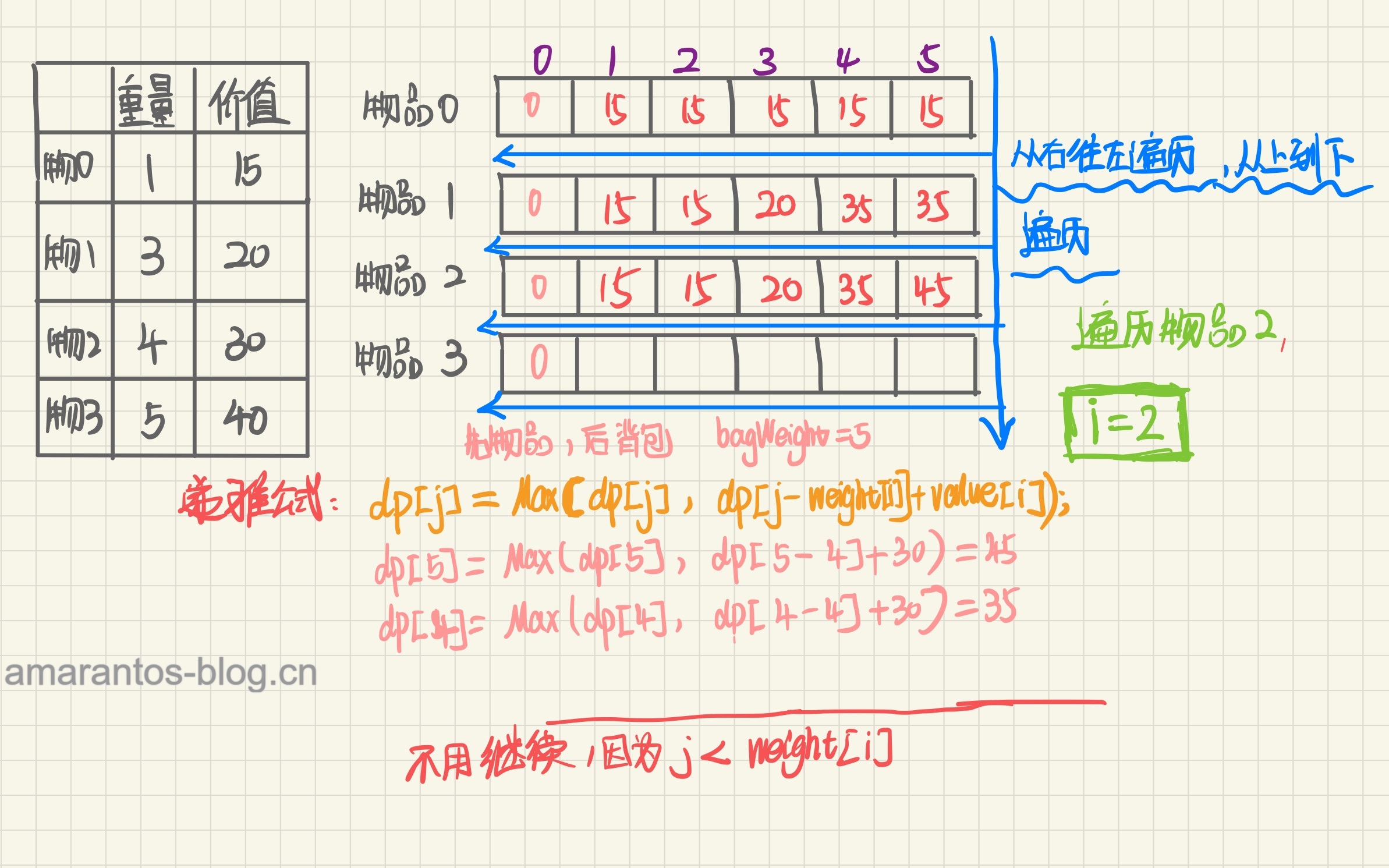
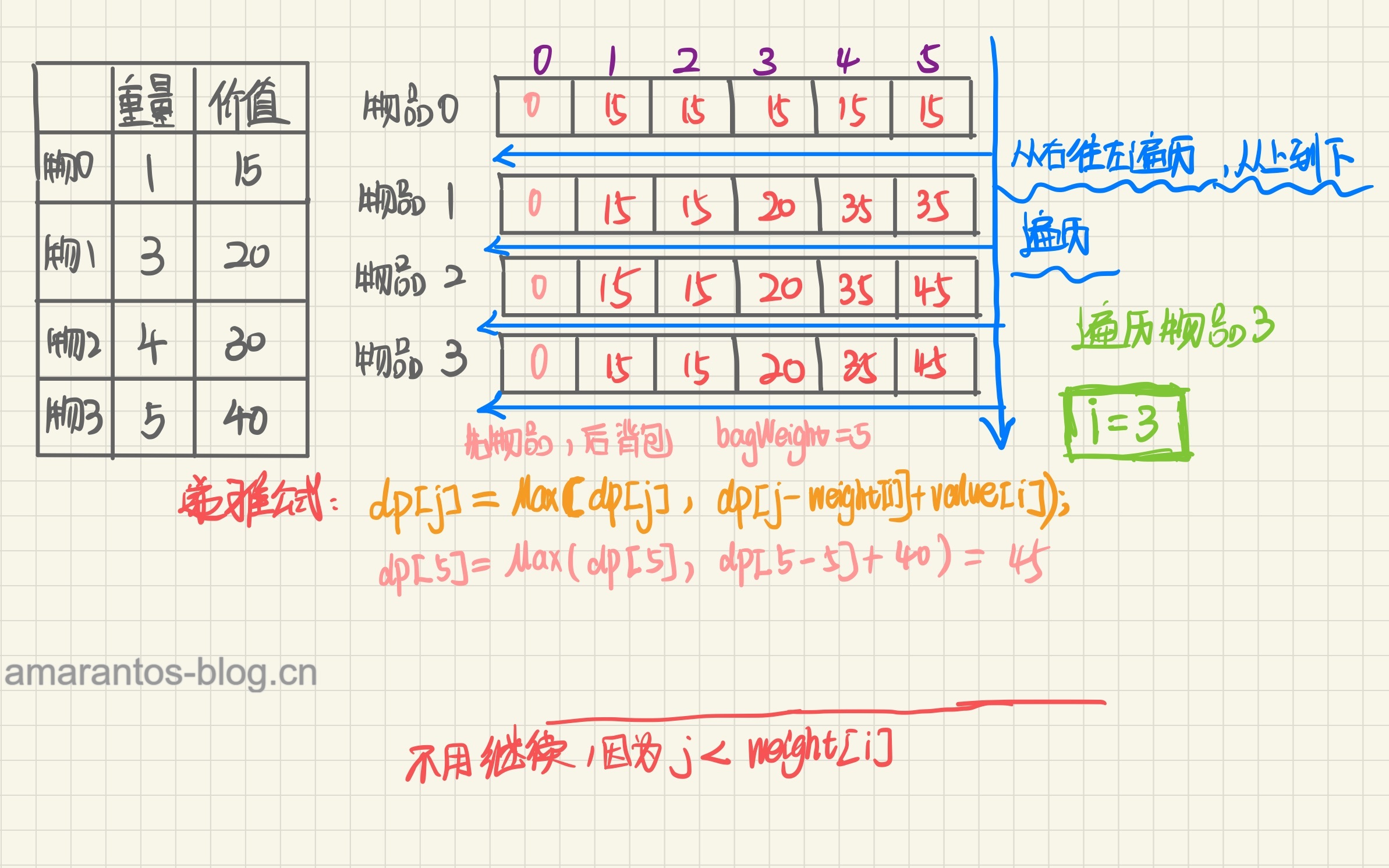
相信走完一遍流程之后，01背包的滚动数组有了更深刻的理解！如果还有不懂的，欢迎评论！

代码实现

 public static void main(String[] args) {
        int[] weight = {1, 3, 4，5};
        int[] value = {15, 20, 30，40};
        int bagWight = 5;
        testWeightBagProblem(weight, value, bagWight);
    }

    public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
        int wLen = weight.length;
        //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
        int[] dp = new int[bagWeight + 1];
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 0; i < wLen; i++){
            for (int j = bagWeight; j >= weight[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        //打印dp数组
        for (int j = 0; j <= bagWeight; j++){
            System.out.print(dp[j] + " ");
        }
    }