Leetcode 77. 组合（画图分析）

力扣传送门(opens new window)

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

解题思路：

这道题我们怎么做呢？

给 1，2，3，4四个数，找出所有组合

[ [1,2], [1,3], [1,4]，[2,3], [2,4], [3,4] ]

这道题我们使用回溯法！

回溯法是一种通过逐步构建解决方案的算法。在组合问题中，我们通常需要遍历每一种情况，这个时候回溯算法就很有用，不知道大家有没有这种感觉，回溯算法其实就是for+递归进行暴力遍历。

也就是我们取1，剩余的2，3，4和1进行挨个组合得到[1,2], [1,3], [1,4]

我们取2，剩余的3，4 和 2 进行挨个组合得到[2,3], [2,4]

我们取3，剩余的4和3进行组合得到[3,4]。

回溯算法：递归+for循环 。

下面讲一下具体的思路：

我们可以从第一个数开始选取，然后递归地选择下一个数，直到选择了 k 个数。当选择了 k 个数后，我们就得到了一个组合（递归结束条件）。然后，我们回溯到上一步，尝试选择其他的数，直到遍历完所有可能的组合。

以下是一个使用回溯法解决该问题的详细步骤：

1. 创建一个列表 res 来保存所有的组合,创建一个构建组合的链表 path。
2. 创建一个辅助函数 backtracking，该函数接受当前正在构建的组合 path、当前可选择的起始位置 begin 和剩余需要选择的数的个数 k。接着我们如何控制取2的时候 ，剩余的数没有1呢，我们就可以使用begain这个变量控制for循环的开始循环大小来实现。
3. 递归结束条件：在 backtracking 函数中，如果 k == path.size()，表示已经选择了 k 个数，将 pre 添加到 res 中，并返回。
4. 否则，从 begin 开始遍历到 n，对于每一个数 i，将其添加到 path 中，并递归调用 backtrack，传入 i+1 作为下一次选择的起始位置。
5. 在递归调用返回后，将刚刚添加的数从 path 中移除，继续遍历下一个数。
6. 在主函数中，调用 backtracking 函数，传入空列表作为当前组合、1 作为起始位置和 k 作为剩余需要选择的数的个数。
7. 返回 res，即为所有可能的组合。

具体的可以看下面的分析图：

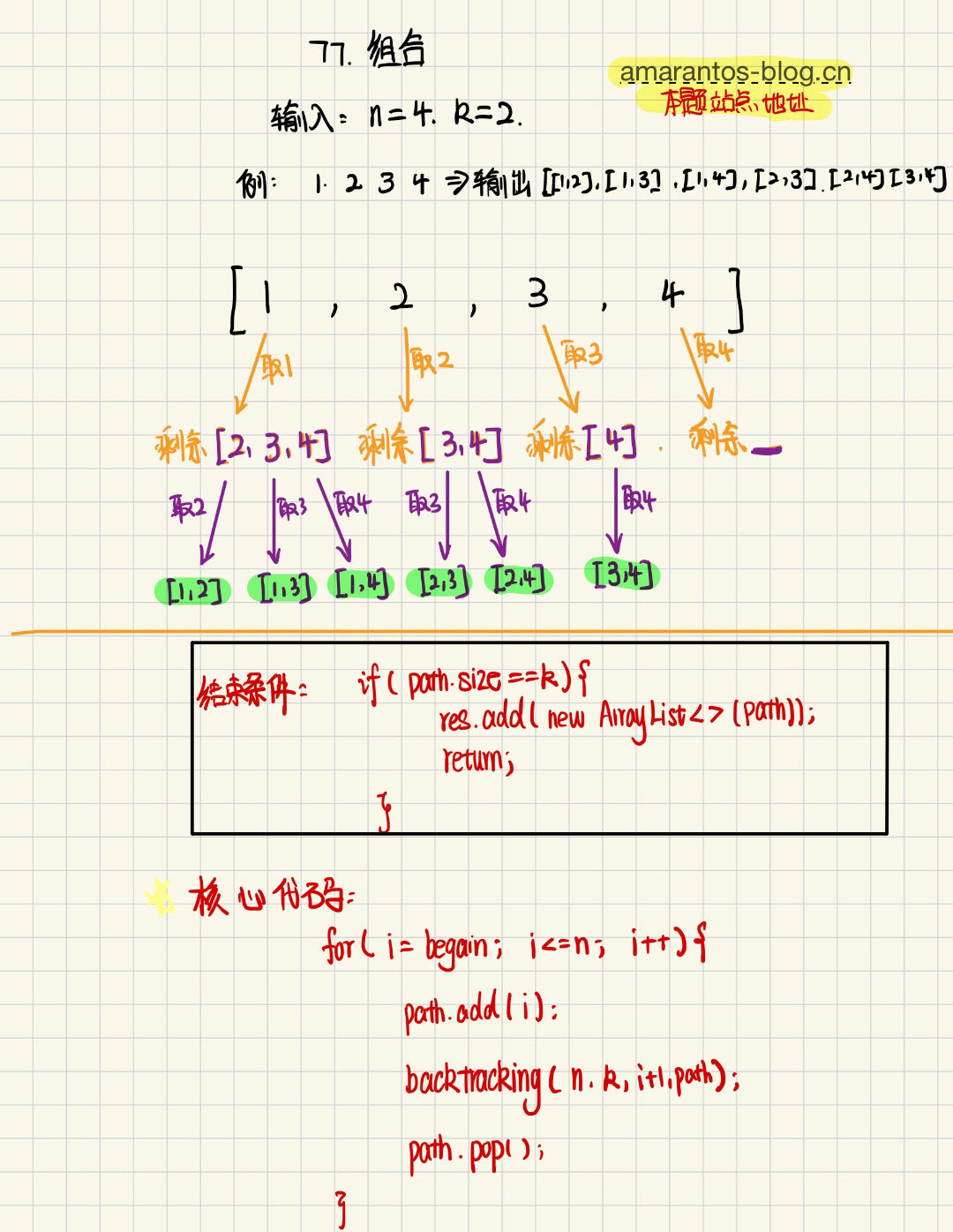
可以看到，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。

第一次取1，剩下集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

接着取2，剩下集合变为3，4。我们只需要再取一个数就可以了，分别取3，4，得到集合[2,3] [2,4] 以此类推。

这样做的目的是不取重复的数，如果我们取2，剩下的集合变成1，3，4，那么我们得到的集合为[2,1][2,3][2,4],但是我们上面已经得到了[1,2]，组合中[2,1]和[1,2]是一样的。

接着我们往下看：

我刚开始没有理解pop()的作用，pop的作用就是当我们取到[1,2]时，把 2 pop() 出去，让 3 add() 进去，这样我们就又得到一个集合[1,3],以此类推。下面来演示一下执行过程：

代码实现：

class Solution {
    // 存储最终结果的列表
    List<List<Integer>> result = new ArrayList<>();  
    // 存储当前路径的链表
    LinkedList<Integer> path = new LinkedList<>();  

    public List<List<Integer>> combine(int n, int k) {
        // 调用回溯函数
        backtracking(n, k, 1);  
        // 返回最终结果列表
        return result;  
    }

    public void backtracking(int n, int k, int begain) {
        // 如果当前路径长度等于 k，表示找到了一个组合
        if (path.size() == k) {  
            // 将当前路径添加到结果列表中
            result.add(new ArrayList<>(path));  
            // 结束当前的回溯递归
            return;  
        }
        // 从 begain 开始遍历数字
        for (int i = begain; i <= n; i++) {  
            // 将当前数字添加到路径中
            path.add(i);  
            // 递归调用，继续向下搜索
            backtracking(n, k, i + 1);  
            // 回溯，将最后一个添加的数字移除，继续考虑下一个数字
            path.removeLast();  
        }
    }
}