Leetcode 46.全排列

力扣传送门(opens new window)

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

• 输入: [1,2,3]
• 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

解题思路：

1. 问题理解：首先，我们需要明确题目的要求和输入。题目要求是给定一个不含重复数字的整数数组，要求生成这个数组所有可能的排列。
2. 回溯算法：针对这种求解所有可能情况的问题，一种常用的解决方法是回溯算法。回溯算法通过尝试所有可能的选择来构建解，并在每一步进行选择之后，进一步探索下一个选择。
3. 递归函数：我们可以使用递归函数来实现回溯算法。在递归函数中，我们需要传入三个参数：原始数组 nums，记录数字是否被使用的标记数组 used，以及当前排列的列表 list。
4. 终止条件：在递归函数中，我们首先需要确定终止条件。当当前排列的长度等于原始数组的长度时，说明我们已经生成了一个完整的排列，我们将其加入结果集合 res 中。
5. 选择列表：在每一步的递归中，我们需要选择一个数字加入当前排列。这个选择的范围是原始数组中尚未被使用的数字。
6. 做出选择：我们依次尝试选择每个未被使用的数字，并将其标记为已使用。然后，将该数字加入当前排列的列表中。
7. 递归调用：接下来，我们递归调用函数，生成下一个位置的数字。在递归调用返回后，我们需要进行回溯操作，即恢复数字的未使用状态，并移除当前位置的数字。
8. 循环遍历：重复上述步骤，直到遍历完所有的选择。每次循环都会生成一个新的排列，直到得到所有可能的排列。
9. 返回结果：最后，当所有的排列都生成完毕后，我们将结果集合 res 返回。

通过以上步骤，我们可以利用回溯算法递归地生成所有可能的排列，并将其存储在结果集合中。

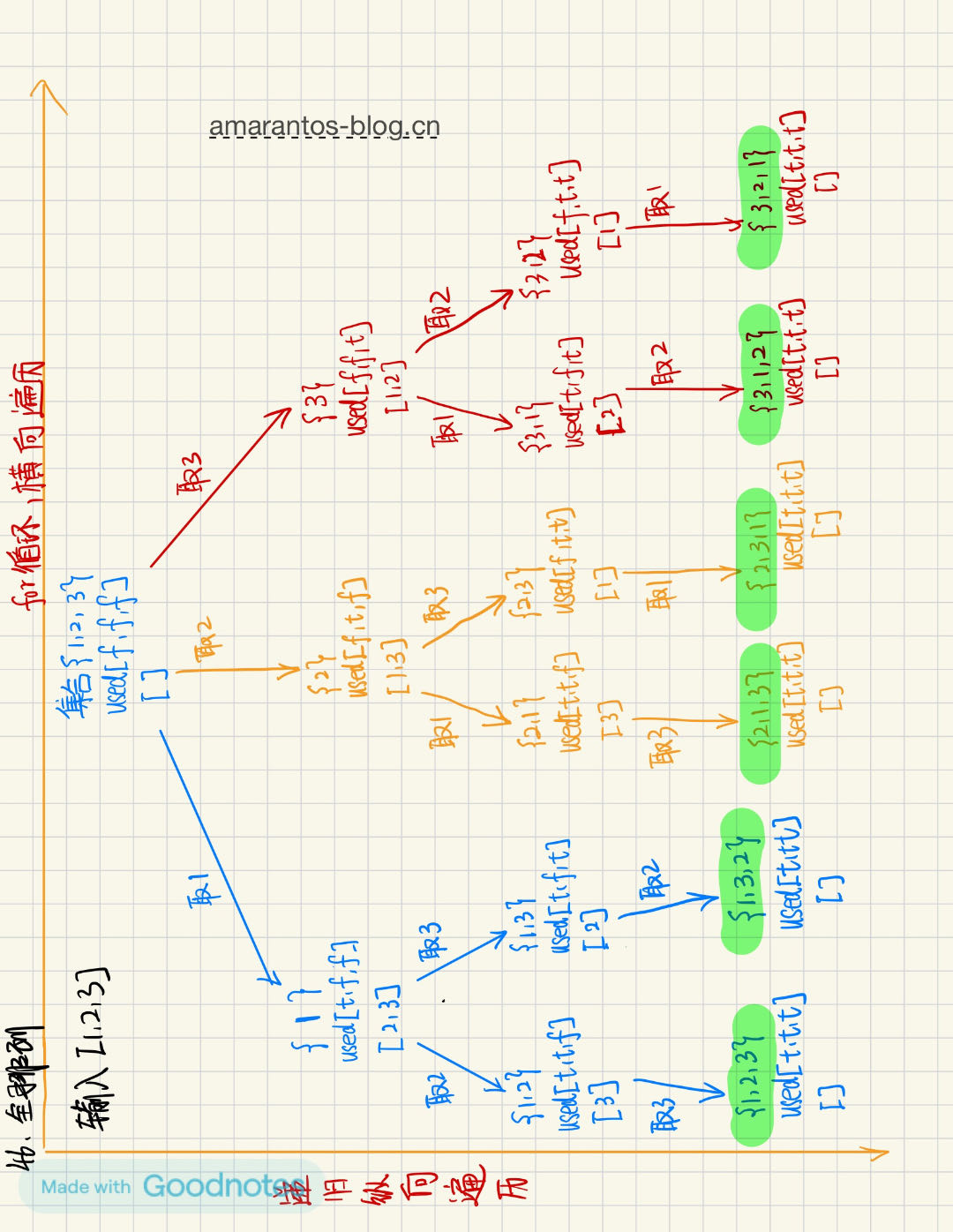
其实思路理清楚之后，不知道大家有没有这样一种疑惑，就是这个树运行流程是怎么样的？其实大家一定要自己走一遍程序，刚开始我也走了好几遍，才把代码流程走通。

以下是以表格形式展示输入 [1, 2, 3] 的前三个排列的生成过程和结果：

当前数字	使用状态	当前排列	剩余集合
-	[false, false, false]	[]	[]
取1	[true, false, false]	[1]	[2,3]
取2	[true, true, false]	[1, 2]	[3]
取3	[true, true, true]	[1, 2, 3]	[1, 2, 3]
回溯	[true, true, false]	[1, 2]	[3]
回溯	[true,false, false]	[1]	[2,3]
取3	[true, false,true]	[1,3]	[2]
取2	[true,true,true]	[1,3,2]	[]
回溯	[true, false,true]	[1,3]	[2]
回溯	[true, false,false]	[1]	[2,3]
回溯	[false, false,false]	[]	[1,2,3]
取2	[false, true,false]	[2]	[1,3]
取1	[true, true,false]	[2,1]	[3]
取3	[true, true,true]	[2,1,3]	[]

在表格中，"使用状态" 列表示数字的使用情况，使用 true 表示数字已被使用，false 表示数字未被使用。"当前排列" 列显示当前的排列。这里我就不写完了，只跟踪了前三个结果，感兴趣的可以跟着代码走一遍，其中有很小的细节需要注意～

最终，结果集合中包含所有可能的排列：

[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]

代码实现：

class Solution {
    // 存储结果的全局变量
    List<List<Integer>> res = new ArrayList(); 

    public List<List<Integer>> permute(int[] nums) {
        if (nums == null || nums.length == 0) {
            return res;
        }
        // 存储当前排列的列表
        List<Integer> list = new ArrayList(); 
        // 记录数字是否被使用过的标记数组
        boolean[] used = new boolean[nums.length]; 
        backTracking(nums, used, list);
        return res;
    }

    public void backTracking(int[] nums, boolean[] used, List<Integer> list) {
        if (list.size() == nums.length) {
            // 当排列的长度等于原始数组的长度时，将当前排列加入结果集合
            res.add(new ArrayList(list)); 
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                // 如果数字已经被使用过，则跳过该数字
                continue; 
            }
            // 标记数字为已使用
            used[i] = true; 
            // 将数字加入当前排列
            list.add(nums[i]); 
            // 递归生成下一个位置的数字
            backTracking(nums, used, i + 1, list); 
            // 恢复数字的未使用状态，以便尝试其他可能性
            used[i] = false; 
            // 移除当前位置的数字，以便尝试其他数字
            list.remove(list.size() - 1); 
        }
    }
}