Leetcode 37. 解数独

力扣传送门(opens new window)

37.Sudoku Solver.

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则： 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。

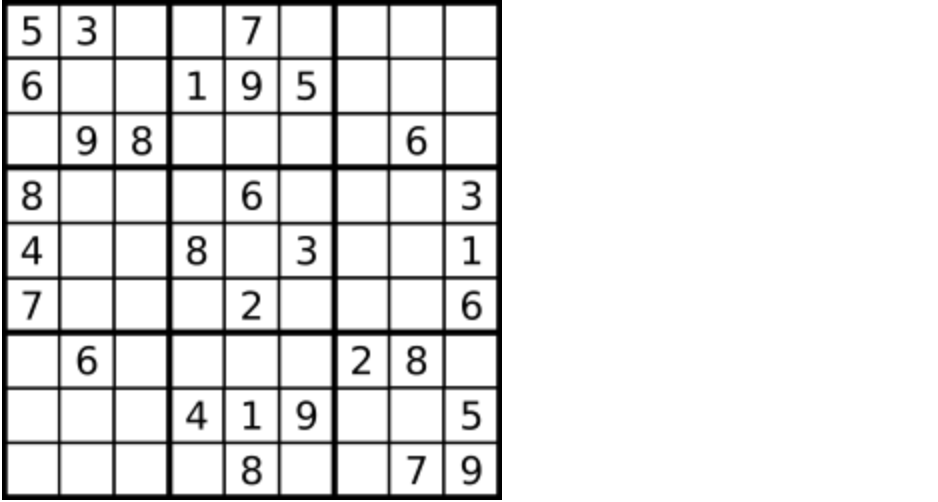
一个数独。

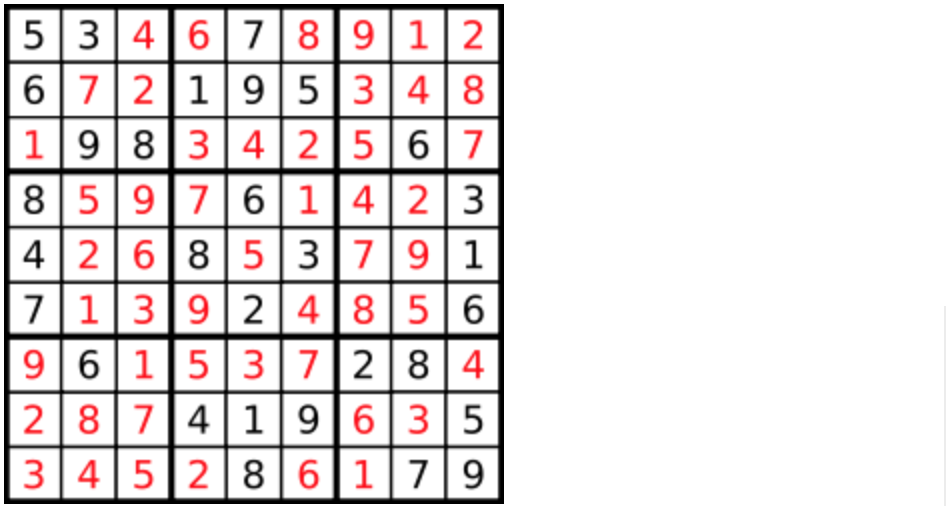
答案被标成红色。

提示：

• 给定的数独序列只包含数字 1-9 和字符 '.' 。
• 你可以假设给定的数独只有唯一解。
• 给定数独永远是 9x9 形式的。

解题思路：

解题思路如下：

1. 定义一个函数 solveSudoku，用于解决数独问题。
2. 在 solveSudoku 函数中，遍历数独的每个位置。
3. 如果当前位置是空白格（用 '.' 表示），则尝试填入数字 1-9，并检查是否满足数独规则。
   • 如果满足数独规则，则将该位置填入数字，并递归调用 solveSudoku 处理下一个位置。
   • 如果不满足数独规则，则回溯到上一步，尝试其他数字。
4. 当所有位置都填满数字时，表示数独问题已解决，返回解决方案。
5. 最终返回解决方案。

九宫格坐标计算方法：

当检查数独中的 3x3 宫格是否有重复数字时，我们需要确定当前位置所在的宫格的起始行和起始列。

以数独中的左上角为原点，每个宫格的索引可以表示为 (startRow, startCol)，其中 startRow 和 startCol 的取值范围为 0、3、6。

具体计算方法如下：

• 对于行，我们可以通过 (row / 3) * 3 来计算宫格的起始行。例如，如果当前位置的行索引 row 是 2，那么 (row / 3) * 3 的结果是 0，表示该宫格的起始行是第 0 行。
• 对于列，我们可以通过 (col / 3) * 3 来计算宫格的起始列。例如，如果当前位置的列索引 col 是 5，那么 (col / 3) * 3 的结果是 3，表示该宫格的起始列是第 3 列。

然后，我们可以使用两个嵌套的循环来遍历当前宫格内的所有位置 (i, j)，其中 i 的取值范围是 0 到 2，表示宫格内的行索引偏移量，j 的取值范围也是 0 到 2，表示宫格内的列索引偏移量。

通过将起始行 startRow 和起始列 startCol 加上相应的偏移量，我们可以得到当前宫格内的具体位置 (startRow + i, startCol + j)。

然后，我们检查该位置上的数字是否与目标数字 num 相同。如果有相同的数字，就意味着该宫格内存在重复数字，应返回 false。如果没有重复数字，则继续遍历其他位置。

这样，我们就可以在循环中检查 3x3 宫格是否有重复数字，并正确判断数独问题的解答是否有效。

代码实现：

public class Solution {
    public void solveSudoku(char[][] board) {
        solve(board);
    }

    private boolean solve(char[][] board) {
        for (int row = 0; row < 9; row++) {
            for (int col = 0; col < 9; col++) {
                if (board[row][col] == '.') {
                    for (char num = '1'; num <= '9'; num++) {
                        if (isValid(board, row, col, num)) {
                            board[row][col] = num;
                            if (solve(board)) {
                                return true;
                            } else {
                                board[row][col] = '.'; // 回溯
                            }
                        }
                    }
                    return false; // 所有数字都尝试过都不符合条件，返回 false
                }
            }
        }
        return true; // 所有位置都填满数字，返回 true
    }

    private boolean isValid(char[][] board, int row, int col, char num) {
        // 检查行中是否有重复数字
        for (int i = 0; i < 9; i++) {
            if (board[row][i] == num) {
                return false;
            }
        }
        // 检查列中是否有重复数字
        for (int j = 0; j < 9; j++) {
            if (board[j][col] == num) {
                return false;
            }
        }
        // 检查 3x3 宫格中是否有重复数字
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (board[startRow + i][startCol + j] == num) {
                    return false;
                }
            }
        }
        return true;
    }
}