Leetcode 101. 对称二叉树

101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

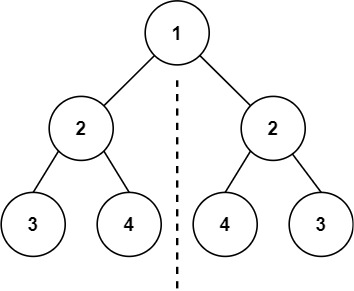
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

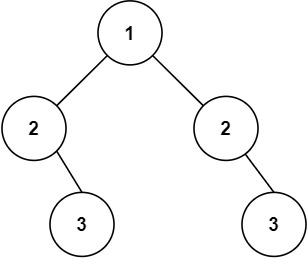
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

解题思路：

所谓对称二叉树，即如下图所示：

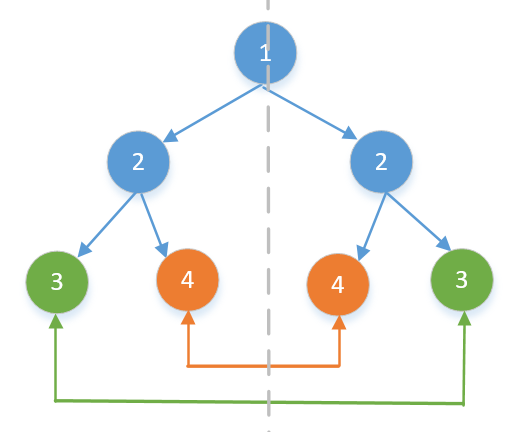
那么，对于任意一对结点leftNode、rightNode，都有这样的性质：

leftNode.val=rightNode.val
rightNode.val=leftNode.val

如果使用递归，我们大可以写出一个判断两个互为镜像位置的结点(leftNode,rightNode)的值是否相等的函数，然后在函数尾部递归调用，来判断镜像结点对(leftNode.left，rightNode.right)以及(leftNode.right，rightNode.left)是否满足性质。

递归终止条件为：

1. 如果左右子节点都为空，认为对称，则返回true
2. 如果左右子节点其中一个为空，认为不对称，则返回false
3. 如果左右子节点的值不相等，认为不对称，则返回false
   可以写出这样的代码：

代码实现：

/**
 * 二叉树节点的定义
 */
public class TreeNode {
    int val; // 节点的值
    TreeNode left; // 左子节点
    TreeNode right; // 右子节点
  
    // 无参构造函数
    TreeNode() {}
  
    // 带值的构造函数
    TreeNode(int val) { this.val = val; }
  
    // 带值和子节点的构造函数
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

// 解决方案类
class Solution {
  
    // 判断二叉树是否对称的方法
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return false; // 如果根节点为空，认为不对称
        }
        return dfs(root.left, root.right); // 调用辅助方法判断左右子树是否对称
    }

    // 深度优先搜索方法，判断左右子树是否对称
    public boolean dfs(TreeNode leftNode, TreeNode rightNode) {
        if (leftNode == null && rightNode == null) {
            return true; // 如果左右子节点都为空，认为对称
        }
        if (leftNode == null || rightNode == null) {
            return false; // 如果左右子节点其中一个为空，认为不对称
        }
        int l = leftNode.val; // 左子节点的值
        int r = rightNode.val; // 右子节点的值
        if (l != r) {
            return false; // 如果左右子节点的值不相等，认为不对称
        }
        // 递归判断左子节点的左子树与右子节点的右子树是否对称，
        // 同时判断左子节点的右子树与右子节点的左子树是否对称
        return dfs(leftNode.left, rightNode.right) && dfs(leftNode.right, rightNode.left);
    }
}