Leetcode 104.二叉树的最大深度

力扣传送门(opens new window)

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例： 给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

解题思路：

树的后序遍历 / 深度优先搜索往往利用 递归 或 栈 实现，本文使用递归实现。

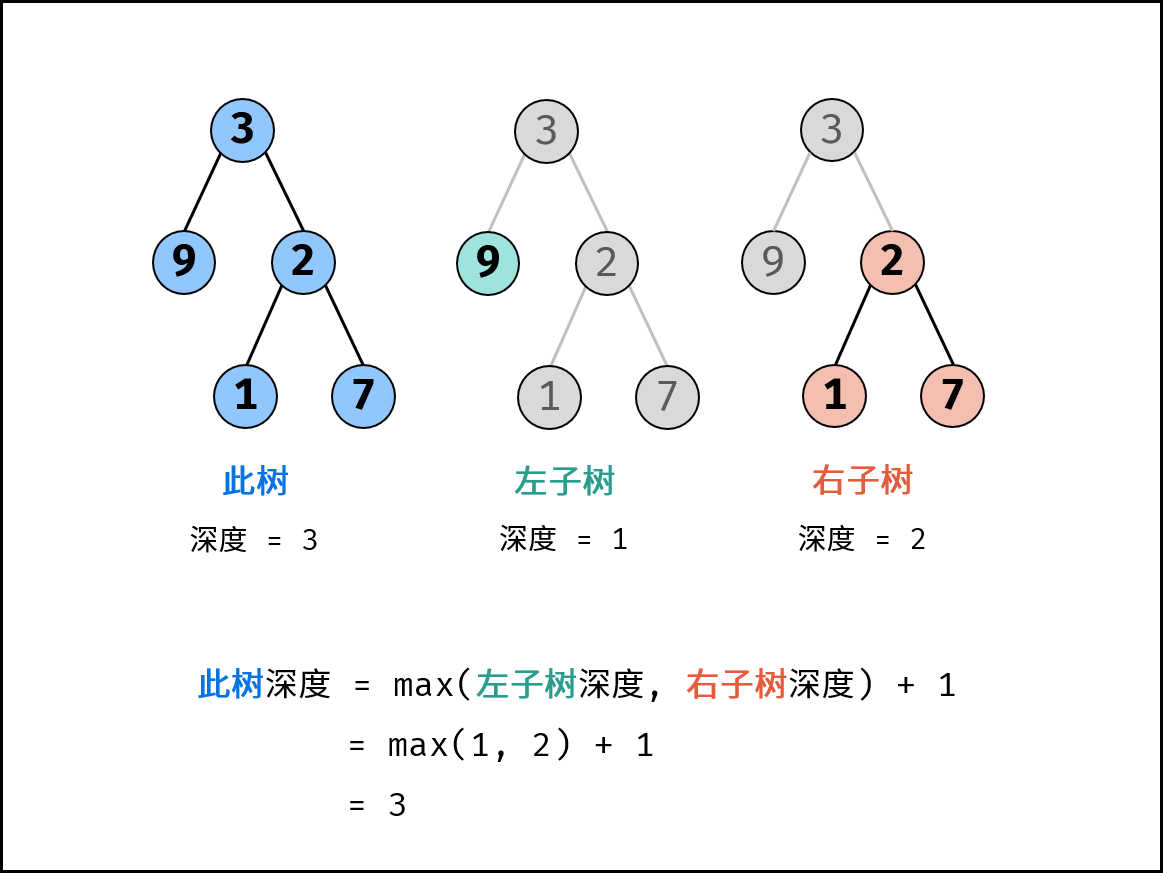
关键点： 此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度 等于 左子树的深度 与 右子树的深度中的 最大值 +1+1+1 。

终止条件： 当 root 为空，说明已越过叶节点，因此返回 深度 000 。
递推工作： 本质上是对树做后序遍历。
计算节点 root 的 左子树的深度 ，即调用 maxDepth(root.left)。
计算节点 root 的 右子树的深度 ，即调用 maxDepth(root.right)。
返回值： 返回 此树的深度 ，即 max(maxDepth(root.left), maxDepth(root.right)) + 1

代码实现：

DFS

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth,rightDepth)+1;
    }
}

BFS:

class Solution {
    int res;
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList();
         queue.add(root);
         while(!queue.isEmpty()){
             int size = queue.size();
             res++;
             while(size-->0){
                 TreeNode currNode = queue.poll();
                 if(currNode.left != null){
                     queue.add(currNode.left);
                 }
                 if(currNode.right != null){
                     queue.add(currNode.right);
                 }
             }
         }
         return res;
    }
}