Leetcode 538.把二叉搜索树转换为累加树

力扣传送门(opens new window)

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。

示例 1：

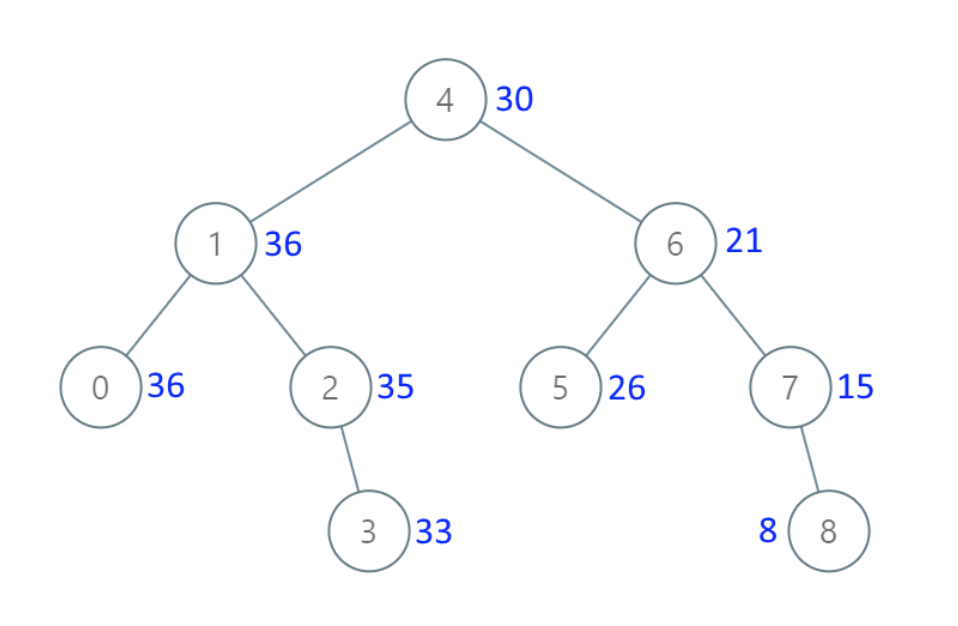
• 输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
• 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

• 输入：root = [0,null,1]
• 输出：[1,null,1]

示例 3：

• 输入：root = [1,0,2]
• 输出：[3,3,2]

示例 4：

• 输入：root = [3,2,4,1]
• 输出：[7,9,4,10]

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

解题思路：

简单来说，题目要求将二叉搜索树中的每个节点的值更新为原值加上大于它的节点值之和，从而得到一个累加树。

1. 对于二叉搜索树，如果将其按照右子树、根节点、左子树的顺序进行中序遍历，得到的结果是一个递增的有序序列。
2. 为了实现将每个节点的值更新为原值加上大于它的节点值之和，可以采用反向的中序遍历（右子树、根节点、左子树的顺序）来遍历二叉搜索树。
3. 在遍历过程中，使用一个变量pre来保存累加值，初始值为0。每遍历一个节点，将当前节点的值加上累加值pre，并更新累加值pre为当前节点的值。
4. 这样，在遍历到某个节点时，累加值pre就是大于它的节点值之和。将当前节点的值更新为原值加上累加值pre即可。
5. 最后完成遍历后，二叉搜索树就被转换为累加树。

代码实现：

class Solution {
    int pre = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root == null){
            return root;
        }
        dfs(root);
        return root;
    }

    // 对二叉搜索树进行深度优先搜索，并实现节点值的累加
    public void dfs(TreeNode root){
        if(root == null){
            return;
        }
        dfs(root.right); // 遍历右子树
      
        root.val += pre; // 将当前节点的值加上累加值pre，使节点值变为原值加上右子树中所有节点的值之和
        pre = root.val; // 更新累加值pre为当前节点的值
      
        dfs(root.left); // 遍历左子树
    }
}

代码跟踪：

例如，给定以下二叉搜索树：

          4
        /   \
       2     6
      / \   / \
     1   3 5   7

将其转换为累加树后，得到：

         22
        /   \
      27     13
     /  \   /  \
   28   25 18   7

1. 首先，我们遍历到节点7，因为它是最右边的节点，没有右子树。所以我们直接将7加上累加值pre（初始为0），得到7+0=7。然后更新累加值pre为7。
2. 接下来，我们遍历到节点6，它有右子树。先递归遍历右子树，即节点7。在遍历右子树后，累加值pre变为7，我们将6加上累加值pre，得到6+7=13。然后更新累加值pre为13。
3. 继续遍历节点6的左子树，即节点5。5+13 = 18。然后更新累加值pre为18。
4. 现在，我们遍历到节点4，它有右子树。先递归遍历右子树，即节点6。在遍历右子树后，累加值pre变为18，我们将4加上累加值pre，得到4+18=22。然后更新累加值pre为22。
5. 继续遍历节点4的左子树，即节点2。先递归遍历右子树，即节点3。在遍历右子树后，累加值pre变为22，我们将3加上累加值pre，得到3+22=25。然后更新累加值pre为25。
6. 继续遍历节点2，我们将2加上累加值pre，得到2+25=27。然后更新累加值pre为27。
7. 最后遍历节点1，我们将1加上累加值pre，得到1+27=28。
8. 当所有节点都被遍历后，二叉搜索树的所有节点的值都会被更新为原值加上大于它的节点值之和，从而得到了累加树。