Leetcode 19.删除链表的倒数第N个节点（画图分析）

力扣传送门(opens new window)

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

进阶：你能尝试使用一趟扫描实现吗？

示例 1：

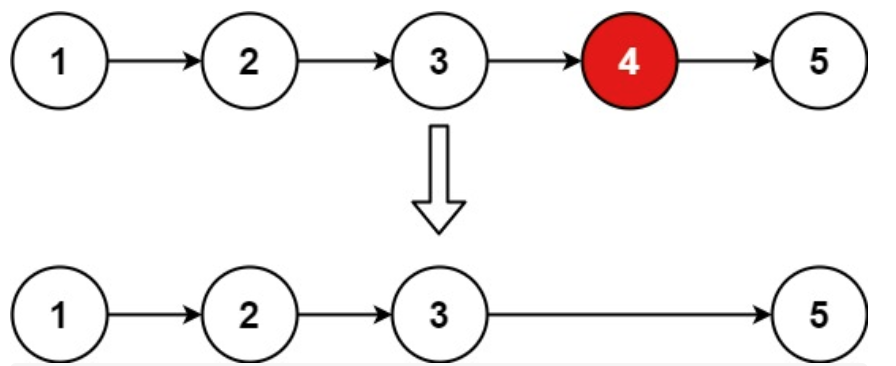
19.删除链表的倒数第N个节点

输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5] 示例 2：

输入：head = [1], n = 1 输出：[] 示例 3：

输入：head = [1,2], n = 1 输出：[1]

解题思路：

这道题真的是老生常谈了，面试的几率非常高，大家要重视这道题。

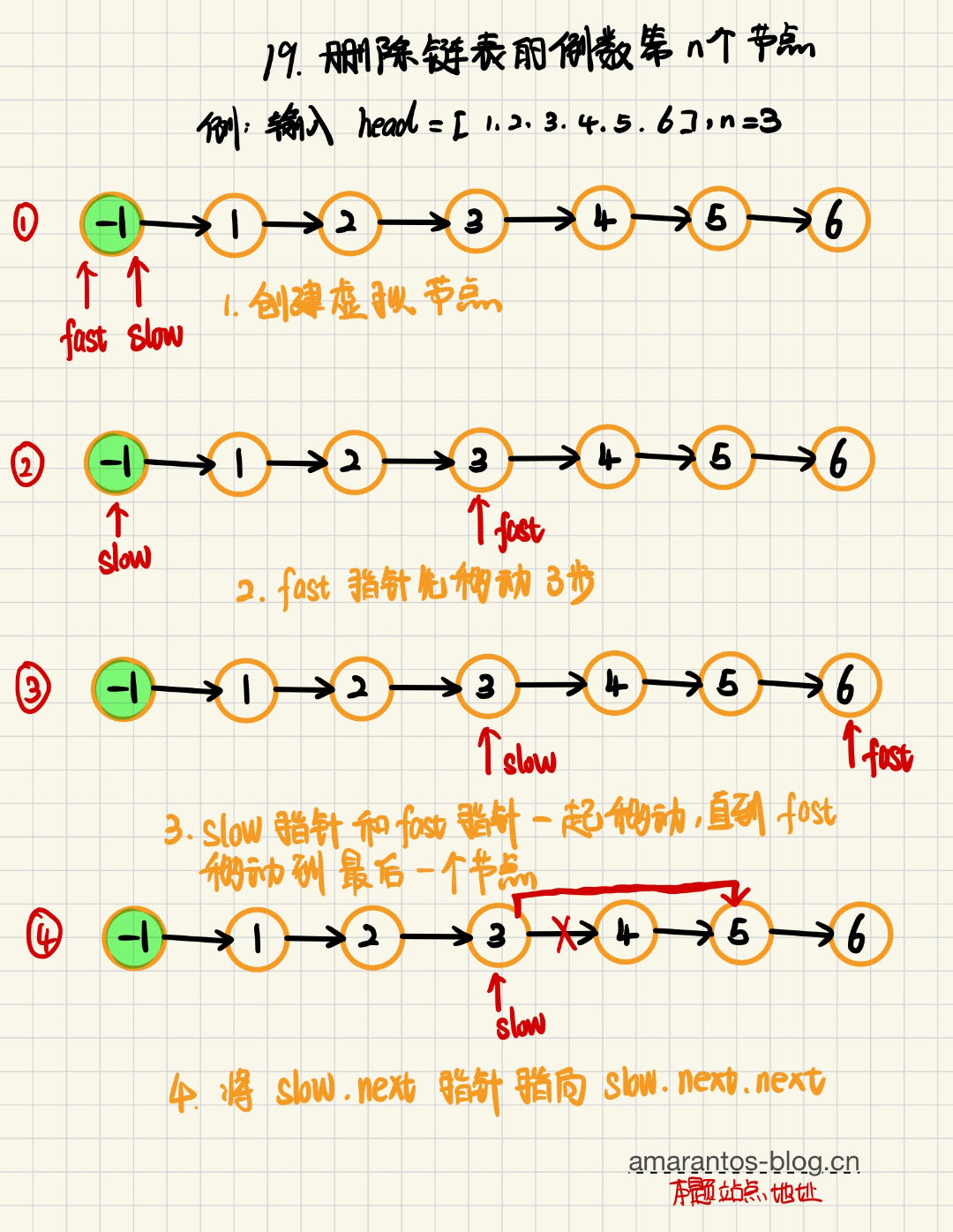
整体思路是让快指针先移动 n 步，之后快慢指针共同移动直到快指针到尾部为止
首先设立虚拟指针 temp
设虚拟指针 temp 的下一个节点指向 head，设快指针为 fast，慢指针为 slow，二者都等于 temp
fast 先向前移动n步，之后 fast 和 slow共同向前移动，此时二者的距离为 n，当 fast 到尾部时，slow 的位置恰好为倒数第 n 个节点，因为要删除该节点，所以要移动到该节点的前一个才能删除，所以循环结束条件为fast.next != null，删除后返回temp.next，为什么不直接返回 head 呢，因为 head 有可能是被删掉的点

以上就是解题思路了，为了便于理解，我们以输入head = [1,2,3,4,5,6], n = 3为例，看一下具体的操作过程。具体操作流程，请见下图所示：

删除链表的倒数第n个节点-oigk.jpg

代码实现：

java

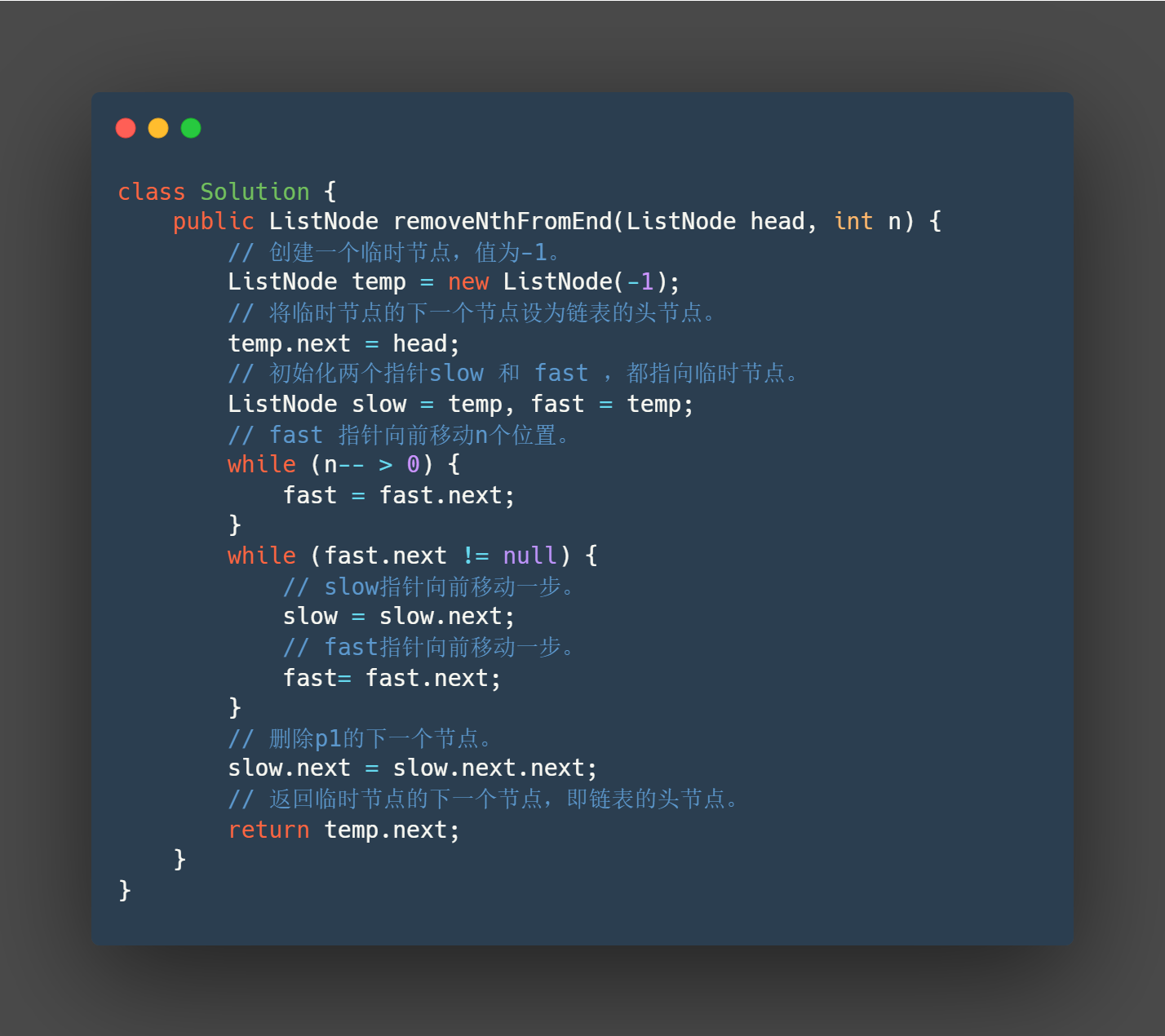
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 创建一个临时节点，值为-1。
        ListNode temp = new ListNode(-1); 
        // 将临时节点的下一个节点设为链表的头节点。
        temp.next = head;
        // 初始化两个指针slow 和 fast ，都指向临时节点。
        ListNode slow = temp, fast = temp; 
        // fast 指针向前移动n个位置。
        while (n-- > 0) {
            fast = fast.next; 
        }
        while (fast.next != null) {
            // slow指针向前移动一步。
            slow = slow.next; 
            // fast指针向前移动一步。
            fast= fast.next; 
        }
        // 删除p1的下一个节点。
        slow.next = slow.next.next; 
        // 返回临时节点的下一个节点，即链表的头节点。
        return temp.next; 
    }
}

python

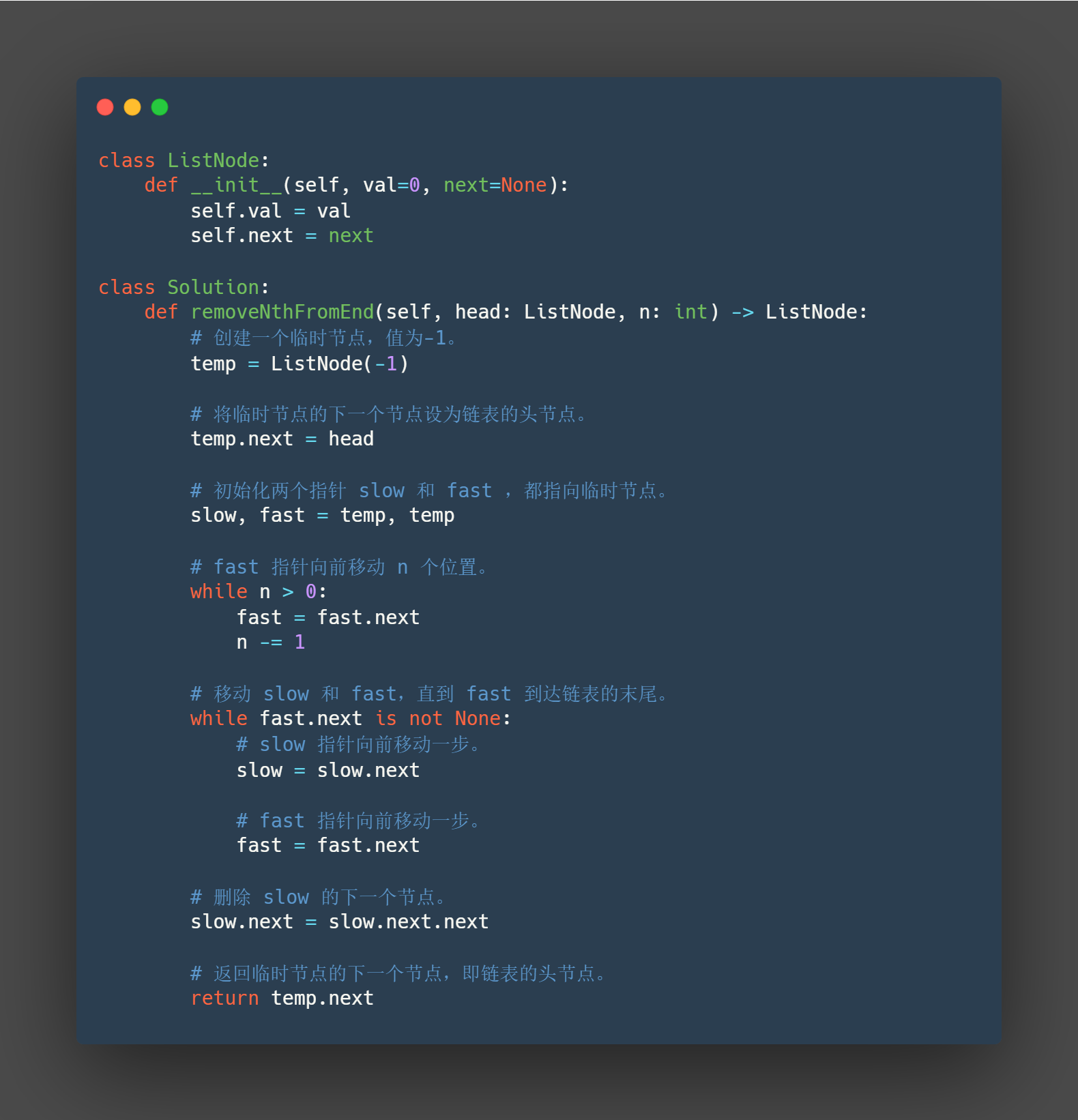
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        # 创建一个临时节点，值为-1。
        temp = ListNode(-1)
      
        # 将临时节点的下一个节点设为链表的头节点。
        temp.next = head
      
        # 初始化两个指针 slow 和 fast ，都指向临时节点。
        slow, fast = temp, temp
      
        # fast 指针向前移动 n 个位置。
        while n > 0:
            fast = fast.next
            n -= 1
      
        # 移动 slow 和 fast，直到 fast 到达链表的末尾。
        while fast.next is not None:
            # slow 指针向前移动一步。
            slow = slow.next
          
            # fast 指针向前移动一步。
            fast = fast.next
      
        # 删除 slow 的下一个节点。
        slow.next = slow.next.next
      
        # 返回临时节点的下一个节点，即链表的头节点。
        return temp.next

c++

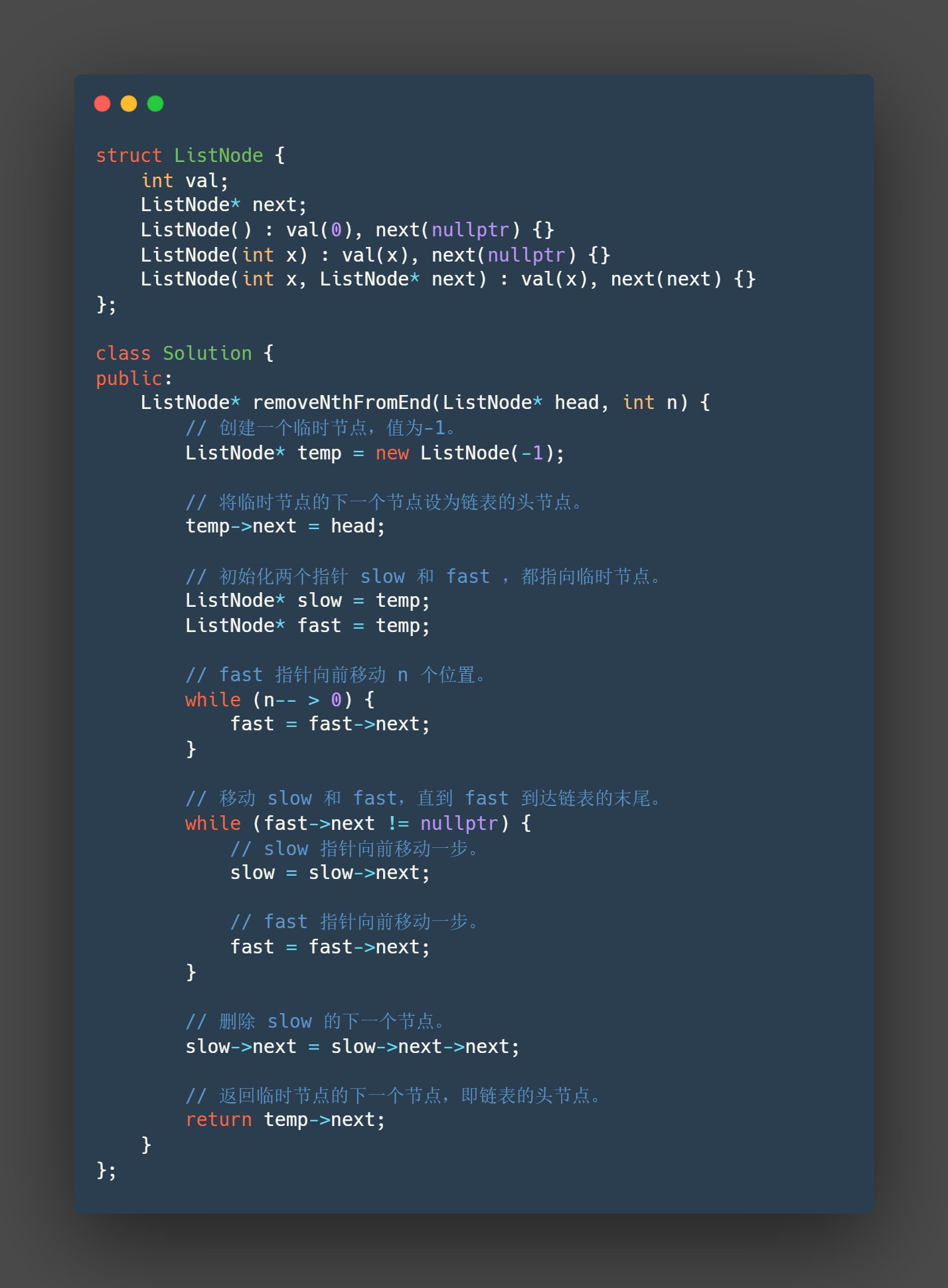
struct ListNode {
    int val;
    ListNode* next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode* next) : val(x), next(next) {}
};

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 创建一个临时节点，值为-1。
        ListNode* temp = new ListNode(-1);
      
        // 将临时节点的下一个节点设为链表的头节点。
        temp->next = head;
      
        // 初始化两个指针 slow 和 fast ，都指向临时节点。
        ListNode* slow = temp;
        ListNode* fast = temp;
      
        // fast 指针向前移动 n 个位置。
        while (n-- > 0) {
            fast = fast->next;
        }
      
        // 移动 slow 和 fast，直到 fast 到达链表的末尾。
        while (fast->next != nullptr) {
            // slow 指针向前移动一步。
            slow = slow->next;
          
            // fast 指针向前移动一步。
            fast = fast->next;
        }
      
        // 删除 slow 的下一个节点。
        slow->next = slow->next->next;
      
        // 返回临时节点的下一个节点，即链表的头节点。
        return temp->next;
    }
};

时间复杂度分析：

在该算法中，最主要的操作是通过两个指针 slow 和 fast 在链表上进行的遍历。具体步骤如下：

移动 fast 指针 n 次：这一步的操作是将 fast 指针向前移动 n 步，时间复杂度为 O(n)。
同时移动 slow 和 fast 指针直到 fast 到达链表末尾：这一步中，fast 从第 n 个节点移动到链表末尾，而 slow 也同时移动。假设链表的长度为 L，那么 fast 需要再走 L-n 步，时间复杂度为 O(L-n)。因此，这一步的时间复杂度也是 O(L)。
删除节点：删除节点的操作是 O(1)，因为只是修改链表指针的指向。

因此，整个算法的时间复杂度为： O(n)+O(L−n)=O(L)O(n) + O(L-n) = O(L)

O(n)+O(L−n)=O(L) 也就是 O(L)，其中 L 是链表的长度。

空间复杂度分析：

该算法使用了两个额外的指针 slow 和 fast，以及一个辅助的临时节点 temp。这都是常数级别的空间开销，与链表的长度无关。

因此，空间复杂度为 O(1)。

目录CONTENT

Leetcode 19.删除链表的倒数第N个节点（画图分析）

Leetcode 19.删除链表的倒数第N个节点（画图分析）

解题思路：

代码实现：

时间复杂度分析：

空间复杂度分析：

评论区