Leetcode 15. 三数之和(画图分析)
- 3Sum
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
注意: 答案中不可以包含重复的三元组。
示例:
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
解题思路:
当解题时,可以按照以下思路来理解和实现这段代码:
-
首先,对给定的整数数组
nums进行排序- 排序可以将数组中的元素按照从小到大的顺序排列,这样可以更方便地进行后续的处理和搜索。
- 排序后,可以使用双指针的方法来搜索满足条件的三元组。排序使得数组中的元素满足递增的顺序,可以通过移动指针来逼近满足条件的解,从而减少搜索的范围和复杂度。
- 排序后,可以通过判断当前元素的值来进行一些优化。比如,在遍历数组时,如果当前元素已经大于 0,那么由于数组已排序,后面的元素都大于 0,因此无论如何组合都不可能凑成满足条件的三元组,可以直接返回结果。
- 排序后,重复元素会相邻排列,这样可以方便地进行去重操作。通过比较当前元素与前一个元素是否相等,可以避免生成重复的三元组,从而减少最终结果中的重复项。
-
对于每一个元素
nums[i],作为可能的三元组的第一个元素(a),尝试找到另外两个元素(b和c),使得a + b + c = 0。 -
在遍历数组时,如果当前元素
nums[i]大于 0,那么由于数组已排序,后面的元素都大于 0,因此无论如何组合都不可能凑成满足条件的三元组,直接返回结果。 -
在遍历数组时,如果当前元素
nums[i]与前一个元素相同(即重复元素),则跳过该元素,以避免生成重复的三元组。(这里想一想为什么nums[i]不和后一个元素比较呢?) -
使用两个指针
left和right分别指向当前元素的下一个元素和数组末尾元素。通过移动指针来搜索满足条件的b和c。 -
当
nums[i] + nums[left] + nums[right]大于 0 时,说明当前的nums[right]太大,需要将right指针左移,减小当前和。 -
当
nums[i] + nums[left] + nums[right]小于 0 时,说明当前的nums[left]太小,需要将left指针右移,增大当前和。 -
当
nums[i] + nums[left] + nums[right]等于 0 时,说明找到了满足条件的三元组。将该三元组添加到结果列表中,并进行去重操作。- 去重逻辑包括:跳过重复的
b元素,即当nums[left] == nums[left + 1]时,将left指针右移; - 跳过重复的
c元素,即当nums[right] == nums[right - 1]时,将right指针左移。
- 去重逻辑包括:跳过重复的
-
在循环结束后,返回结果列表,其中包含了所有满足条件的三元组。
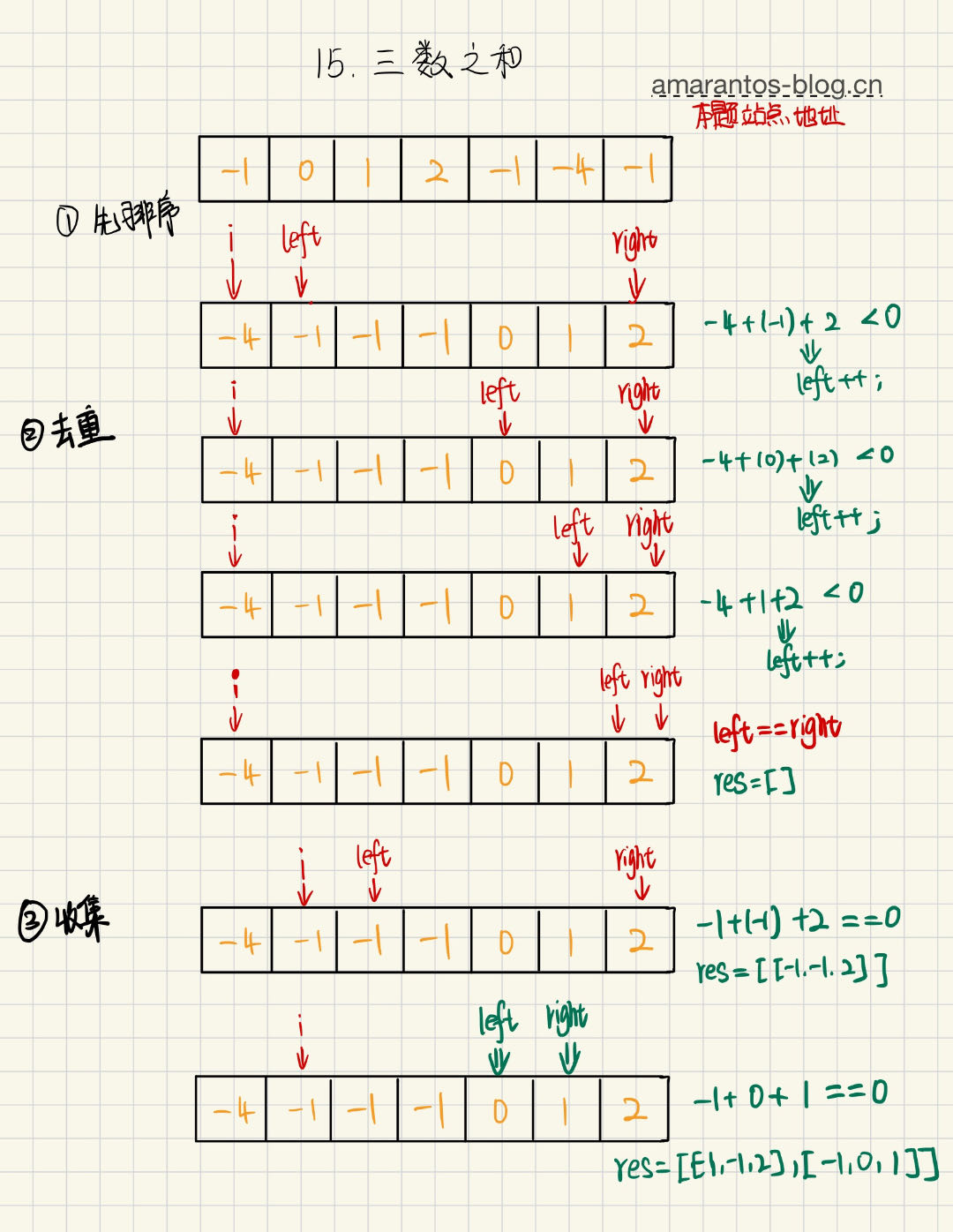
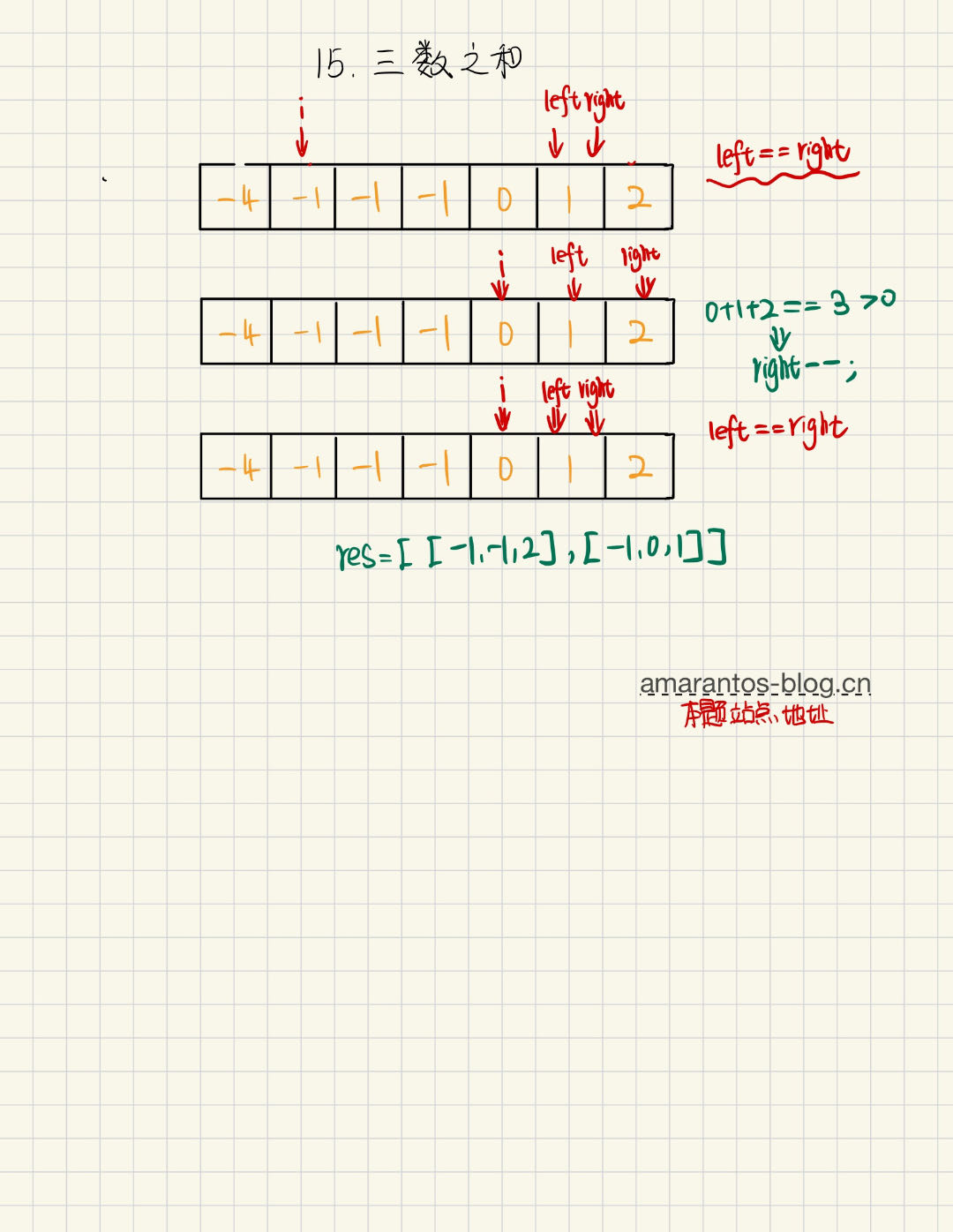
下面是动态图演示
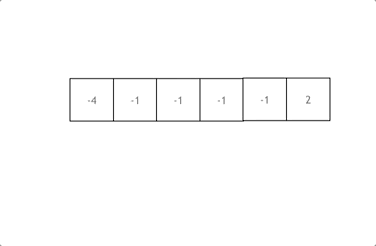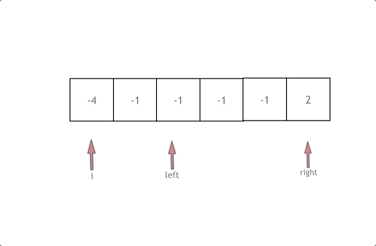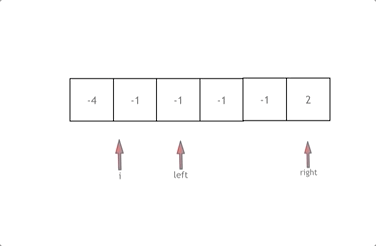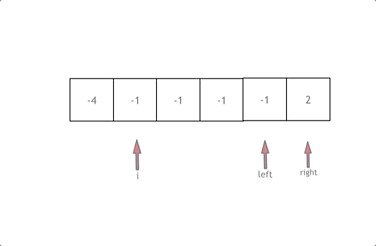
代码实现:
java
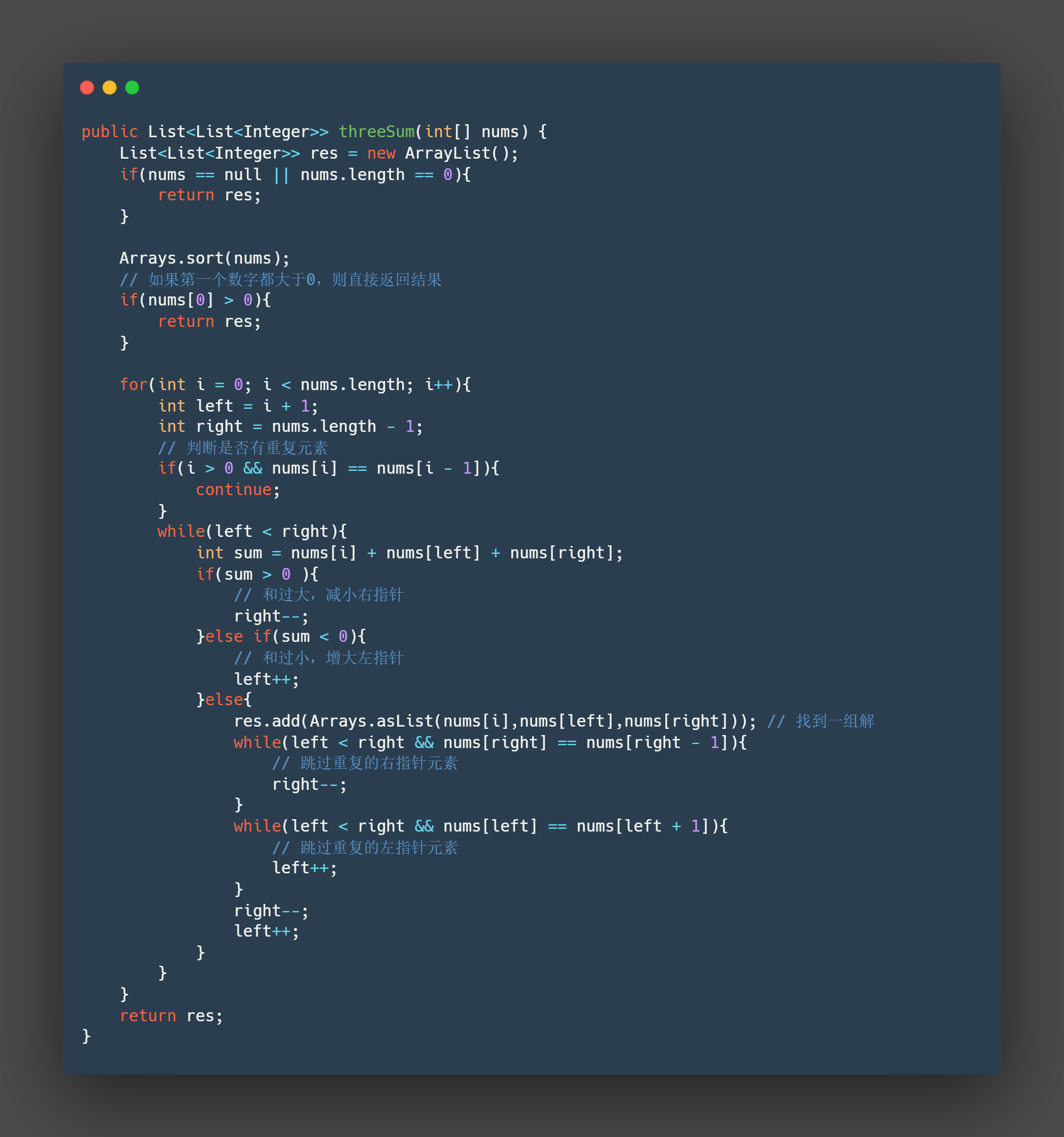
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList();
if(nums == null || nums.length == 0){
return res;
}
Arrays.sort(nums);
// 如果第一个数字都大于0,则直接返回结果
if(nums[0] > 0){
return res;
}
for(int i = 0; i < nums.length; i++){
int left = i + 1;
int right = nums.length - 1;
// 判断是否有重复元素
if(i > 0 && nums[i] == nums[i - 1]){
continue;
}
while(left < right){
int sum = nums[i] + nums[left] + nums[right];
if(sum > 0 ){
// 和过大,减小右指针
right--;
}else if(sum < 0){
// 和过小,增大左指针
left++;
}else{
res.add(Arrays.asList(nums[i],nums[left],nums[right])); // 找到一组解
while(left < right && nums[right] == nums[right - 1]){
// 跳过重复的右指针元素
right--;
}
while(left < right && nums[left] == nums[left + 1]){
// 跳过重复的左指针元素
left++;
}
right--;
left++;
}
}
}
return res;
}
python3
from typing import List
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = []
if not nums or len(nums) == 0:
return res
# 对数组进行排序
nums.sort()
if nums[0] > 0:
# 如果最小数大于 0,直接返回
return res
for i in range(len(nums)):
if i > 0 and nums[i] == nums[i - 1]:
# 跳过重复的元素
continue
# 定义双指针
left, right = i + 1, len(nums) - 1
while left < right:
# 计算三数之和
sum = nums[i] + nums[left] + nums[right]
if sum > 0:
# 如果和大于 0,移动右指针
right -= 1
elif sum < 0:
# 如果和小于 0,移动左指针
left += 1
else:
# 找到一组解
res.append([nums[i], nums[left], nums[right]])
while left < right and nums[left] == nums[left + 1]:
# 跳过重复的左指针
left += 1
while left < right and nums[right] == nums[right - 1]:
# 跳过重复的右指针
right -= 1
left += 1
right -= 1
return res
c++
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> res;
if (nums.empty()) {
return res;
}
// 对数组进行排序
sort(nums.begin(), nums.end());
if (nums[0] > 0) {
// 如果最小数大于 0,直接返回
return res;
}
for (int i = 0; i < nums.size(); ++i) {
if (i > 0 && nums[i] == nums[i - 1]) {
// 跳过重复的元素
continue;
}
// 定义双指针
int left = i + 1, right = nums.size() - 1;
while (left < right) {
// 计算三数之和
int sum = nums[i] + nums[left] + nums[right];
if (sum > 0) {
// 如果和大于 0,移动右指针
right--;
} else if (sum < 0) {
// 如果和小于 0,移动左指针
left++;
} else {
// 找到一组解
res.push_back({nums[i], nums[left], nums[right]});
// 跳过重复的左指针
while (left < right && nums[left] == nums[left + 1]) left++;
// 跳过重复的右指针
while (left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
}
}
}
return res;
}
};
时间复杂度
- 排序的时间复杂度:
- 对 nums 进行排序需要 O(N log N) 的时间。
- 双指针查找部分:
- 在排序后的数组中,外层循环从 0 到 N-1,时间复杂度是 O(N)。
- 对于每一个 i,双指针的部分需要 O(N) 的时间(左指针和右指针每次移动一次,共需最多 N 次移动)。
- 因此,整体双指针部分的时间复杂度是 O(N²)。
综合来看,这道题的时间复杂度为 O(N²)。排序的 O(N log N) 相对较小,因此整体主导时间复杂度是 O(N²)。
空间复杂度
- 输入数组存储:输入数组 nums 占用 O(N) 的空间。
- 返回结果的存储:结果集 res 是存储三元组的二维数组,最坏情况下,空间复杂度可以达到 O(K),其中 K 是返回的三元组的个数。
- 排序过程的辅助空间:如果使用原地排序,空间复杂度为 O(1);如果使用其他非原地排序算法,可能需要 O(N) 的辅助空间。
总空间复杂度:最坏情况下为 O(N + K),其中 N 是输入数组的长度,K 是结果集中三元组的个数。




评论区