Leetcode 416. 分割等和子集（画图分析）

力扣传送门(opens new window)

题目难易：中等

416 。PartitionEqualSubsetSum

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意: 每个数组中的元素不会超过 100 数组的大小不会超过 200

示例 1:

输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.

提示：

1 <= nums.length <= 200
1 <= nums[i] <= 100

解题思路：

01背包问题

背包问题，大家都知道，有N件物品和一个最多能背重量为W 的背包。

第 i 件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、分组背包和混合背包等等。

要注意题目描述中商品是不是可以重复放入。

即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包，写法还是不一样的。

简单举例

我们先举一个简单的01背包的例子

问题描述：

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

这里为了让大家容易联想，我举了几个易于区分重量和价值的物品，

水的重量为1，价值为3
书的重量为3，价值为4
相机的重量为4，价值为5

而我们的背包最大容量为5。

首先我们将背包的最大容量 5 分为0，1，2，3，4，5的顺序作为该表格的内容

物品分别有三样，分别是水，书本，和相机，因此我们的行为3，第0行代表了物品为空

需要注意的是，在01背包问题下，每个物品只能取一次或者不取，不能同时选择同一种物品

所以，组成的二维数组即是dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。换句话说，每个表格是当前条件下的最优解

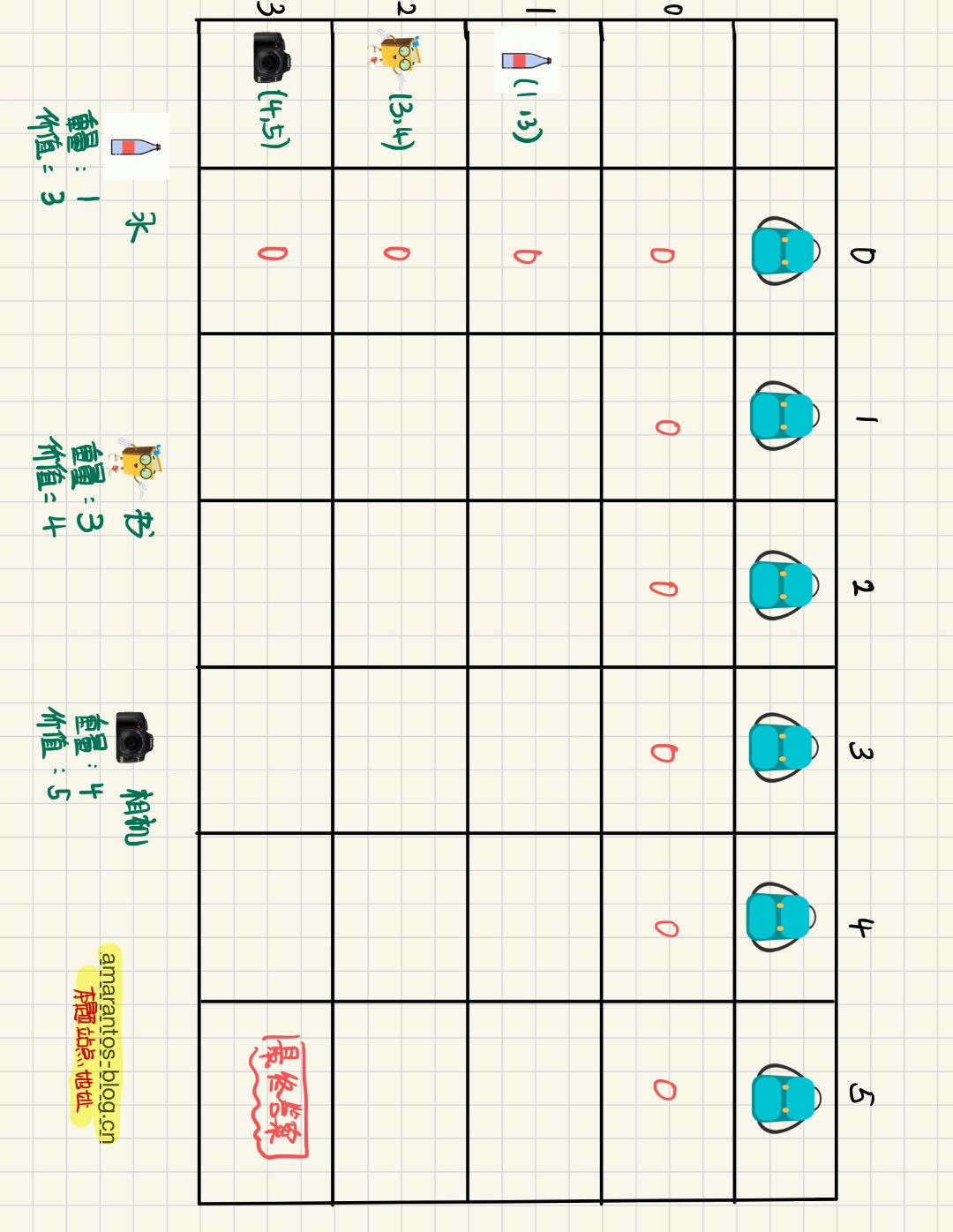
分割等和子集1.jpg

首先看第0行

对于第0行来说，由于第0行没有任何物品，因此，在任何的背包容量下，他的价值总和最优解都为0.

同样的，针对第0列，由于背包容量为0，任何物品都无法放入，所有他的价值总和最优解也都为0。

那么最后一行的最后一列的单元格，即是我们需要求解的最终答案。

下面我们对每一个单元格进行分析！

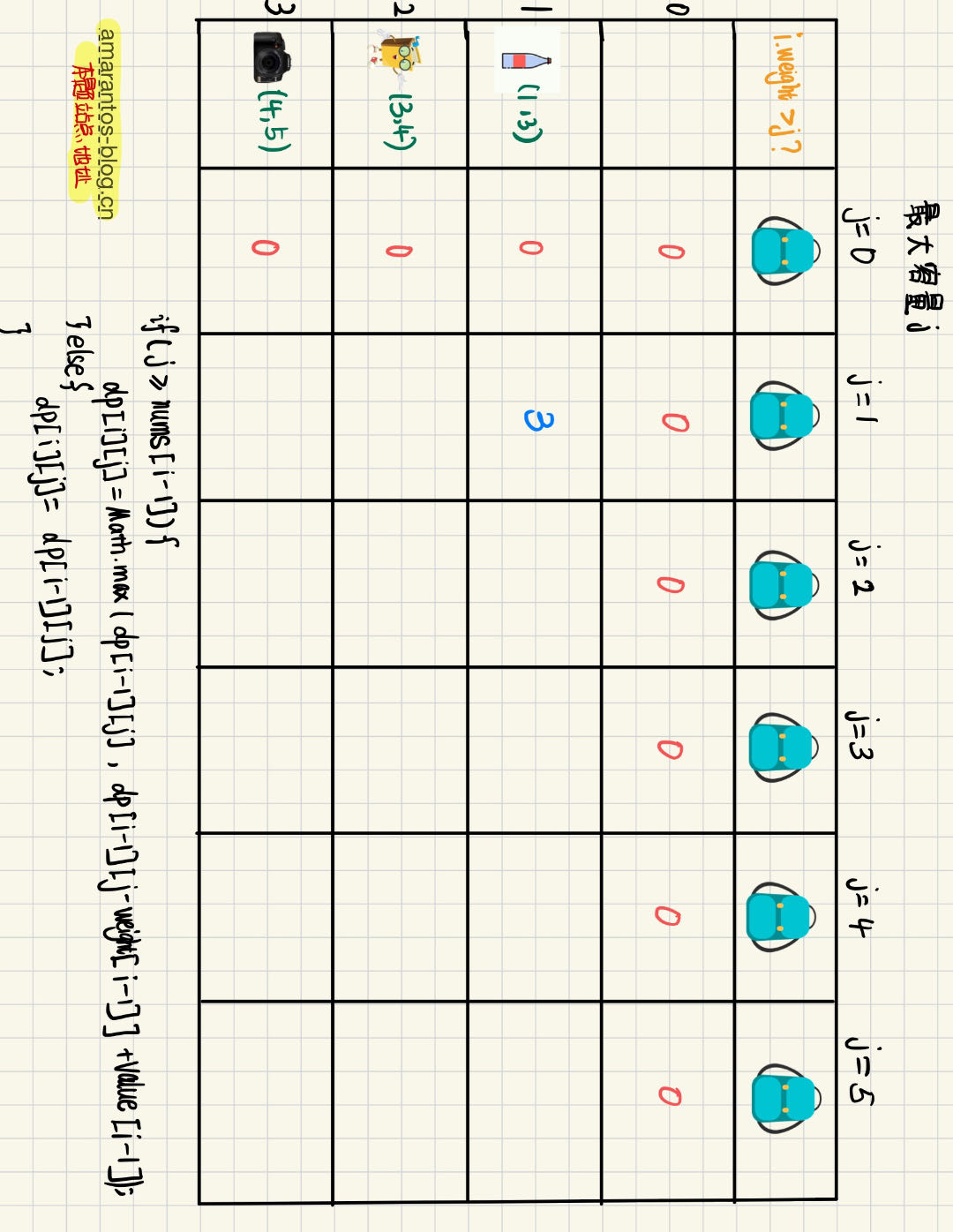
分割等和子集2.jpg

在考虑每一个单元格的时候，我们需要做一次判断，那就是新纳入的物品重量，是否超过了书包的总容量

首先看i=1,j=1的单元格，单元格需要填写的是在背包容量为1的情况下，对前1种物品进行选择获得的最大价值，首先是水的重量为1，书包的最大容量为1，很容易可以看出，我们可以把水放入书包，此时背包的最大价值为3

那么代码是如何判断的呢？

if (j >= weight[i]){
    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
} else{
    dp[i][j] = dp[i - 1][j];
}

此时我们的背包容量大于等于选取的水的重量1，正好可以放进去，所以我们走的第一个判断逻辑

接着我们需要比较不放水的背包的最大价值和放水的背包的最大价值

不放水的背包的最大价值就是 dp[i-1][j]; 此时的 dp[i-1][j] = 0;

放水的背包的最大价值为 dp[i - 1][j - weight[i]] + value[i]

此时的 dp[i - 1][j - weight[i]] + value[i] = 3

选择两组数据中较大的数就是我们想要的答案

所以，我们需要将该单元格的最优解填入为3.

同样的，由于i=1的行只能选择水，所以我们的背包大最优解都为3

下面我们看i=2的一行。

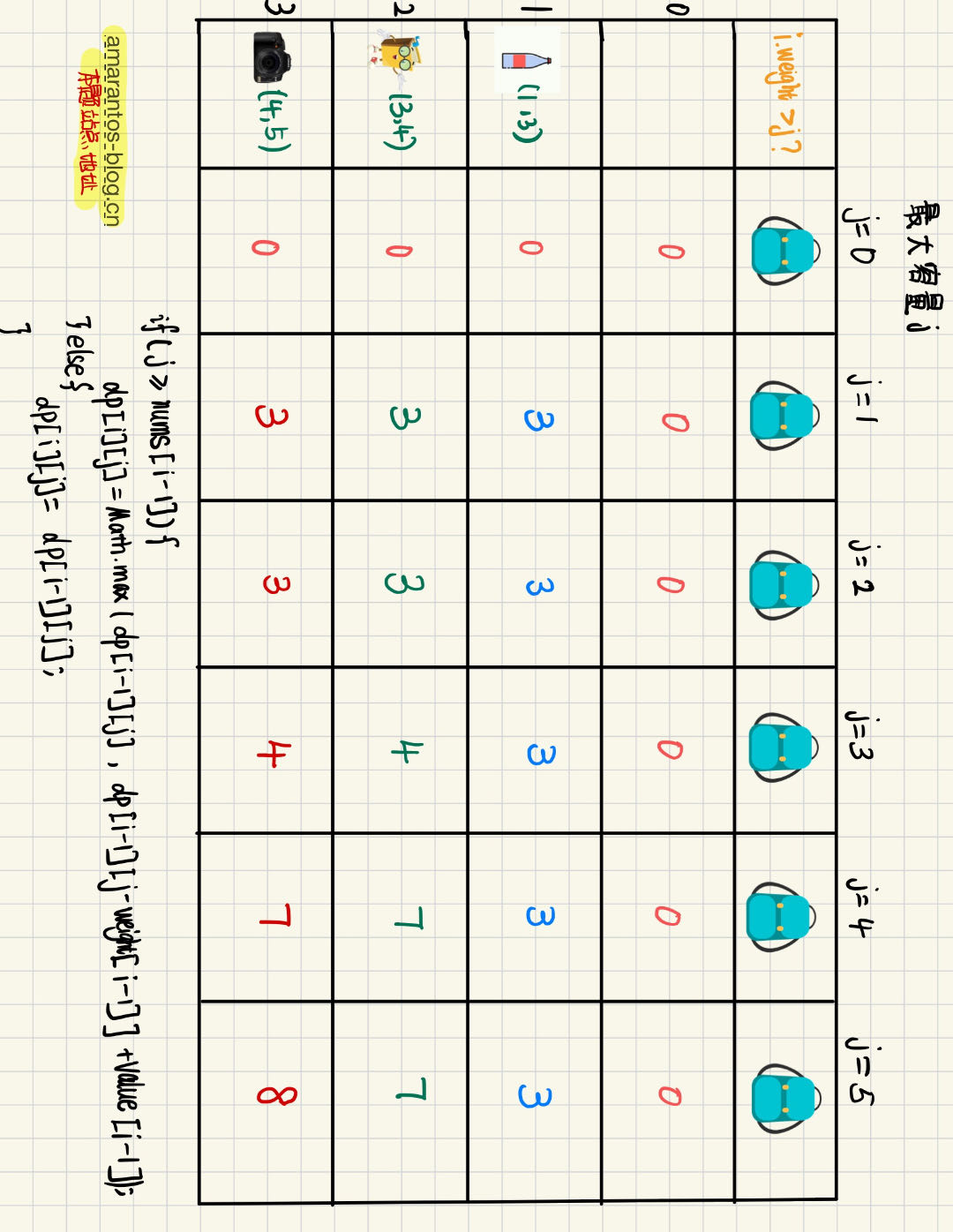
分割等和子集3.jpg

i=2,j=1时

由于书的重量3大于背包的重量1，所以我们只能继承不放入书的情况的最优解，即该单元格上方的值3

i=2,j=2时，同理

由于书的重量3大于背包的重量2，所以我们只能继承不放入书的情况的最优解，即该单元格上方的值3

i=2,j=3时

此时背包容量为3，大于等于书的重量3，我们需要将书纳入是否要放进书包的考量

不放书的情况
- dp[i-1][j] = 3
放书的情况
- dp[i - 1][j - weight[i]] + value[i]
- dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么 dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值
- 此时放书的情况最大价值为4

因此，比较上面两组数据，我们将该单元格填写为4.

i=2,j=4时

此时背包容量为4，大于书的重量3，我们需要将书纳入是否要放进书包的考量

不放书的情况
- dp[i-1][j] = 3
放书的情况
- dp[i - 1][j - weight[i]] + value[i]
- dp[i - 1][j - weight[i]] 为背包容量为1的时候不放物品书的最大价值，那么我们再加上书的价值，即 dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放书得到的最大价值
- 此时放书的情况最大价值为7

因此，比较上面两组数据，我们将该单元格填写为7.

后面大家可以继续延续这个思路继续推导。

最后我们看最后一个单元格

即i=3,j=5的时候

此时背包容量为5，大于相机的重量4，我们需要将相机纳入是否要放进书包的考量

不放相机的情况
- dp[i-1][j] = 7
放相机的情况
- dp[i - 1][j - weight[i]] + value[i]
- dp[i - 1][j - weight[i]] 为背包容量为1的时候不放物品相机的最大价值，那么我们再加上相机的价值，即 dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放相机得到的最大价值
- 此时放书的情况最大价值为8

因此，比较上面两组数据，我们将该单元格填写为8.

大家经过上面的学习是不是对01背包有了更加深刻的了解！！

下面我们回到本题中！！

本题实例讲解

这题判断把数组分成两份，这两份的元素和是否相等。

我们只需要判断是否存在一些元素的和等于sum/2，如果等于sum/2，那么剩下的肯定也等于sum/2

那么这个时候问题就很明朗了，假设sum/2是一个背包的容量，我们只需要找出一些元素把他放到背包中，如果背包中元素的最大和等于sum/2，说明我们可以把数组分成完成相等的两份。这不就是经典的0-1背包问题吗。

首先我们需要计算数组中所有元素的和sum，然后判断sum是否是偶数：

如果不是偶数，说明不可能分割成完全相等的两份，直接返回false。

回归主题：首先，本题要求集合里能否出现总和为 sum / 2 的子集。

那么来一一对应一下本题，看看背包问题如何来解决。

只有确定了如下四点，才能把01背包问题套到本题上来。

背包的体积为sum / 2
背包要放入的商品（集合里的元素）重量为元素的数值，价值也为元素的数值
背包如果正好装满，说明找到了总和为 sum / 2 的子集。
背包中每一个元素是不可重复放入。
注意：本题中物品的重量和价值相等，物品的重量即是物品的价值，物品的价值即是物品的重量

以上分析完，我们就可以套用01背包，来解决这个问题了。

我们在来找一下他的递推公式，定义dp[i][j]表示把第i个物品放到容量为j的背包中所获得的的最大值。

第i个物品的值是nums[i-1]：

如果nums[i-1]>j，说明背包容量不够，第i件物品放不进去，所以我们不能选择第i个物品，那么

dp[i][j]=dp[i-1][j]；

如果nums[i-1]<=j，说明可以把第j个物品放到背包中，我们可以选择放也可以选择不放，取最大值即可，如果放就会占用一部分背包容量，最大价值是

dp[i][j]=dp[i-1][j-nums[i-1]]+nums[i-1]

如果不放

dp[i][j]=dp[i-1][j]；

取两者的最大值

最终递推公式如下

if (j >= nums[i - 1]) {
    dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - nums[i - 1]] + nums[i - 1]);
} else {
    dp[i][j] = dp[i - 1][j];
}

我们来看下最终代码

public boolean canPartition(int[] nums) {
    //计算数组中所有元素的和
    int sum = 0;
    for (int num : nums)
        sum += num;
    //如果sum是奇数，说明数组不可能分成完全相等的两份
    if ((sum & 1) == 1)
        return false;
    //sum除以2
    int target = sum >> 1;
    int length = nums.length;
    int[][] dp = new int[length + 1][target+1];
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            //下面是递推公式
            if (j >= nums[i - 1]) {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - nums[i - 1]] + nums[i - 1]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    //判断背包最大是否能存放和为target的元素
    return dp[length][target] == target;
}

我们还可以这样写，二维数组dp是boolean类型，dp[i][j]表示数组中前i个元素的和是否可以组成和为j，很明显dp[0][0]=true，表示前0个元素（也就是没有元素）可以组成和为0。代码如下

public boolean canPartition(int[] nums) {
    //计算数组中所有元素的和
    int sum = 0;
    for (int num : nums)
        sum += num;
    //如果sum是奇数，说明数组不可能分成完全相等的两份
    if ((sum & 1) == 1)
        return false;
    //sum除以2
    int target = sum >> 1;
    int length = nums.length;
    boolean[][]dp = new boolean[length + 1][target+1];
    dp[0][0] = true;//base case
    for (int i = 1; i <= length; i++) {
        for (int j = 1; j <= target; j++) {
            //递推公式
            if (j >= nums[i - 1]) {
                dp[i][j] = (dp[i - 1][j] || dp[i-1][j - nums[i - 1]]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[length][target];
}

我们看到上面二维数组计算的时候当前值只和上面一行有关，所以我们可以把它改成一维的

分析如下：

确定dp数组以及下标的含义

01背包中，dp[j] 表示：容量为j的背包，所背的物品价值最大可以为dp[j]。

本题中每一个元素的数值既是重量，也是价值。

套到本题，dp[j]表示背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。

那么如果背包容量为target， dp[target]就是装满背包之后的重量，所以当 dp[target] == target 的时候，背包就装满了。

有录友可能想，那还有装不满的时候？

拿输入数组 [1, 5, 11, 5]，举例， dp[7] 只能等于 6，因为只能放进 1 和 5。

而dp[6] 就可以等于6了，放进1 和 5，那么dp[6] == 6，说明背包装满了。

确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。

所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

dp数组如何初始化

在01背包，一维dp如何初始化，已经讲过，

从dp[j]的定义来看，首先dp[0]一定是0。

如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。

这样才能让dp数组在递推的过程中取得最大的价值，而不是被初始值覆盖了。

本题题目中只包含正整数的非空数组，所以非0下标的元素初始化为0就可以了。

确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中就已经说明：如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

就明白了，相当于同一行后面的值依赖前面的，如果不是倒叙，前面的值被修改了，在计算后面的就会导致错误。我们来看下代码。

代码实现：

class Solution {
    public static boolean canPartition(int[] nums) {
        if(nums == null || nums.length == 0) return false;
        int n = nums.length;
        int sum = 0;
        for(int num : nums) {
            sum += num;
        }
        //总和为奇数，不能平分
        if(sum % 2 != 0) return false;
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for(int i = 0; i < n; i++) {
            System.out.println("=========");
            for(int j = target; j >= nums[i]; j--) {
                //物品 i 的重量是 nums[i]，其价值也是 nums[i]
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
                System.out.println("背包总容量(所能装的总重量)是:"+j+"，放进物品后，背的最大重量为 ="+dp[j]);
            }
            //剪枝一下，每一次完成內層的for-loop，立即檢查是否dp[target] == target，優化時間複雜度（26ms -> 20ms）
            if(dp[target] == target)
                return true;
        }
        return dp[target] == target;
    }
}

下面是我打印出的dp

C:\Users\wangyiqing\.jdks\corretto-18.0.2\bin\java.exe "-javaagent:F:\wyq\idea\IntelliJ IDEA 2021.3.3\lib\idea_rt.jar=12104:F:\wyq\idea\IntelliJ IDEA 2021.3.3\bin" -Dfile.encoding=UTF-8 -classpath G:\leetcode\out\production\leetcode leetcode.dynamicprogramming.PartitionEqualSubsetSum
=========
背包总容量(所能装的总重量)是:11，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:10，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:9，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:8，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:7，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:6，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:5，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:4，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:3，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:2，放进物品后，背的最大重量为 =1
背包总容量(所能装的总重量)是:1，放进物品后，背的最大重量为 =1
=========
背包总容量(所能装的总重量)是:11，放进物品后，背的最大重量为 =6
背包总容量(所能装的总重量)是:10，放进物品后，背的最大重量为 =6
背包总容量(所能装的总重量)是:9，放进物品后，背的最大重量为 =6
背包总容量(所能装的总重量)是:8，放进物品后，背的最大重量为 =6
背包总容量(所能装的总重量)是:7，放进物品后，背的最大重量为 =6
背包总容量(所能装的总重量)是:6，放进物品后，背的最大重量为 =6
背包总容量(所能装的总重量)是:5，放进物品后，背的最大重量为 =5
=========
背包总容量(所能装的总重量)是:11，放进物品后，背的最大重量为 =11
true

Process finished with exit code 0

目录CONTENT

Leetcode 416. 分割等和子集（画图分析）

Leetcode 416. 分割等和子集（画图分析）

解题思路：

01背包问题

简单举例

本题实例讲解

代码实现：

评论区