Leetcode 704. 二分查找（画图分析）

力扣传送门(opens new window)

Leetcode 704.binary-search

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

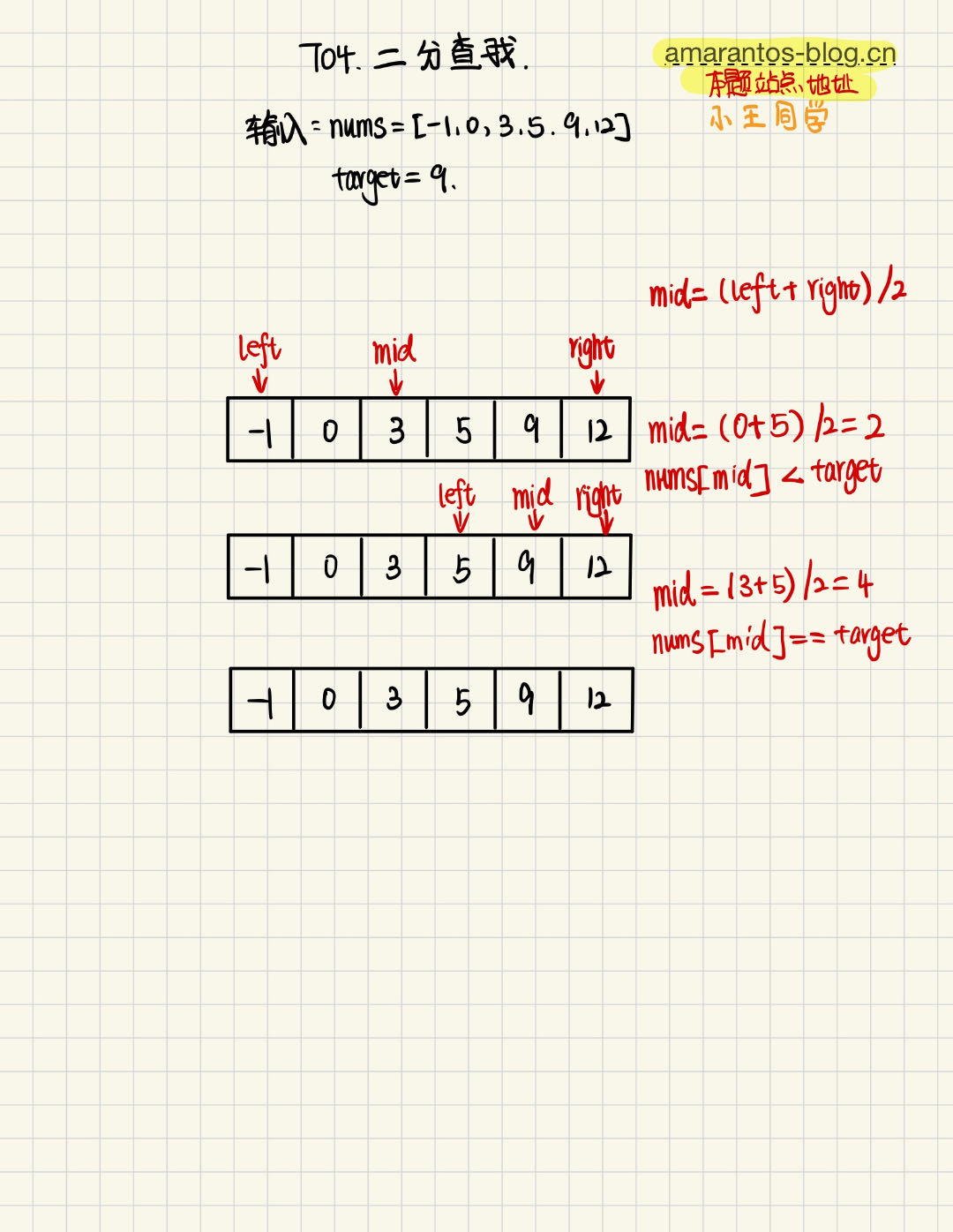
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

Java 源码中的应用

Arrays.binarySearch()

Java的 java.util.Arrays类中提供了 binarySearch()方法，它是一个常见的二分查找实现，用于在有序数组或列表中查找元素。此方法可用于基本类型的数组（如 int[]、long[]）或实现了 Comparable接口的对象。

int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int index = Arrays.binarySearch(arr, 5);  // 返回元素 5 的索引

Collections.binarySearch()

在 java.util.Collections中，也提供了对 List的二分查找方法。与 Arrays.binarySearch()类似，它在有序的 List中查找目标元素的位置，尤其适用于不可变集合的查找操作。

List<Integer> list = Arrays.asList(1, 2, 3, 4, 5, 6, 7, 8, 9);
int index = Collections.binarySearch(list, 5);  // 返回元素 5 的索引

题目解析：

1. 初始化左边界 left 为数组的起始位置，右边界 right 为数组的结束位置。
2. 在每一次循环中，计算中间位置的索引 mid，通过 mid = (left + right) / 2 来获取。
3. 比较中间位置的元素 nums[mid] 与目标值 target 的关系：
   • 如果 nums[mid] 大于 target，说明目标值在左半部分，将右边界 right 更新为 mid - 1，继续在左半部分进行查找。
   • 如果 nums[mid] 小于 target，说明目标值在右半部分，将左边界 left 更新为 mid + 1，继续在右半部分进行查找。
   • 如果 nums[mid] 等于 target，则找到目标值，返回 mid。
4. 在每一次循环中，根据目标值与中间元素的比较结果，不断缩小搜索范围，直到左边界 left 大于右边界 right，表示未找到目标值。
5. 如果循环结束仍然未找到目标值，返回 -1 表示未找到。

关键点在于利用有序数组的特性，通过不断缩小搜索范围，将时间复杂度降低为 O(log n)。二分查找算法在处理大规模的有序数据搜索问题时非常高效。

需要注意的是，二分查找要求目标数组是有序的，如果数组无序，则需要先进行排序操作，再执行二分查找。

代码实现：

java

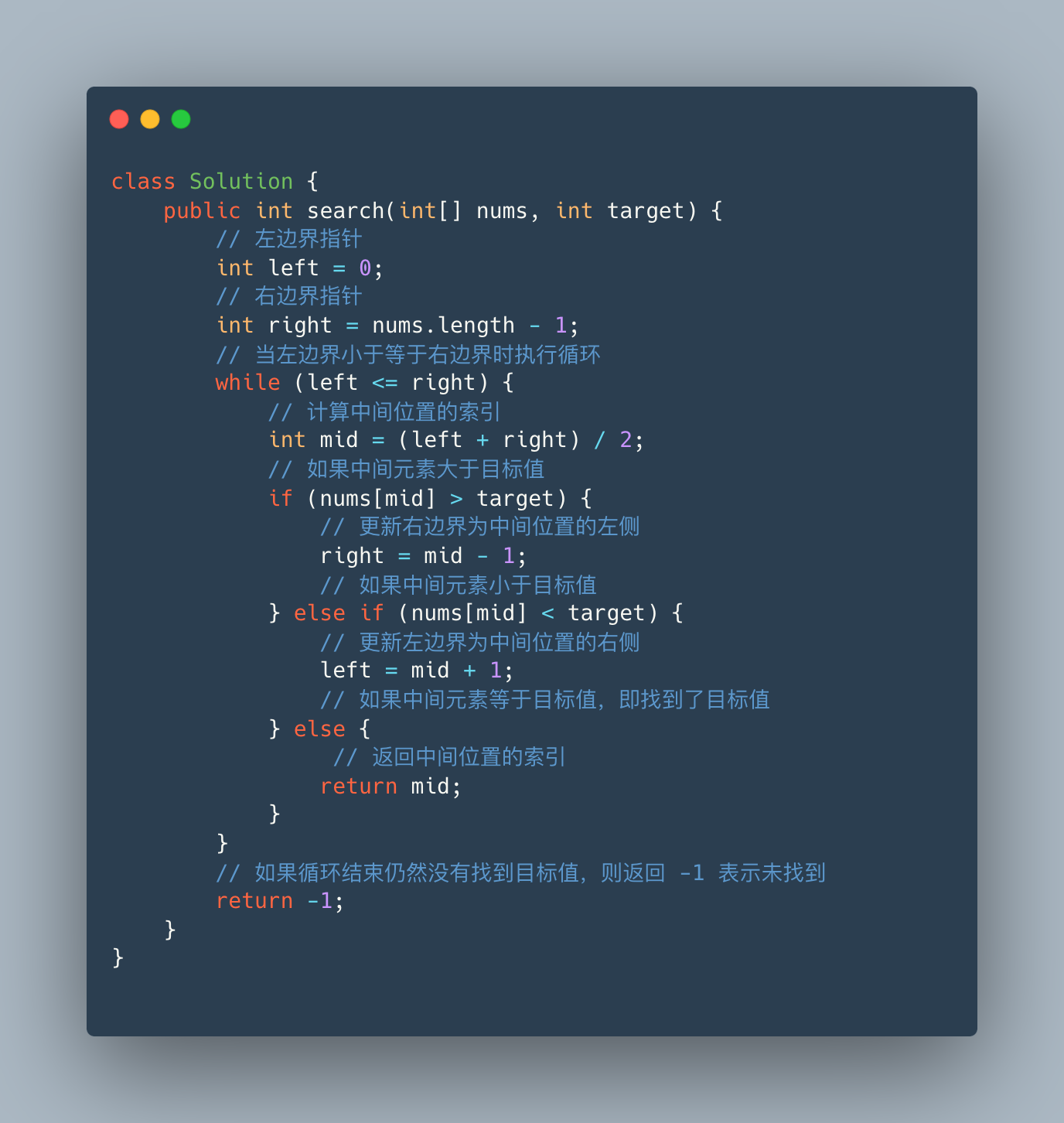
class Solution {
    public int search(int[] nums, int target) {
        // 左边界指针
        int left = 0;  
        // 右边界指针
        int right = nums.length - 1;  
        // 当左边界小于等于右边界时执行循环
        while (left <= right) {  
            // 计算中间位置的索引
            int mid = (left + right) / 2;  
            // 如果中间元素大于目标值
            if (nums[mid] > target) {  
                // 更新右边界为中间位置的左侧
                right = mid - 1;  
                // 如果中间元素小于目标值
            } else if (nums[mid] < target) {  
                // 更新左边界为中间位置的右侧
                left = mid + 1;  
                // 如果中间元素等于目标值，即找到了目标值
            } else {  
                 // 返回中间位置的索引
                return mid; 
            }
        }
        // 如果循环结束仍然没有找到目标值，则返回 -1 表示未找到
        return -1;  
    }
}

python:

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0  # 左边界指针
        right = len(nums) - 1  # 右边界指针

        while left <= right:  # 当左边界小于等于右边界时执行循环
            mid = (left + right) // 2  # 计算中间位置的索引

            if nums[mid] > target:  # 如果中间元素大于目标值
                right = mid - 1  # 更新右边界为中间位置的左侧
            elif nums[mid] < target:  # 如果中间元素小于目标值
                left = mid + 1  # 更新左边界为中间位置的右侧
            else:  # 如果中间元素等于目标值，即找到了目标值
                return mid  # 返回中间位置的索引

        # 如果循环结束仍然没有找到目标值，则返回 -1 表示未找到
        return -1

c++：

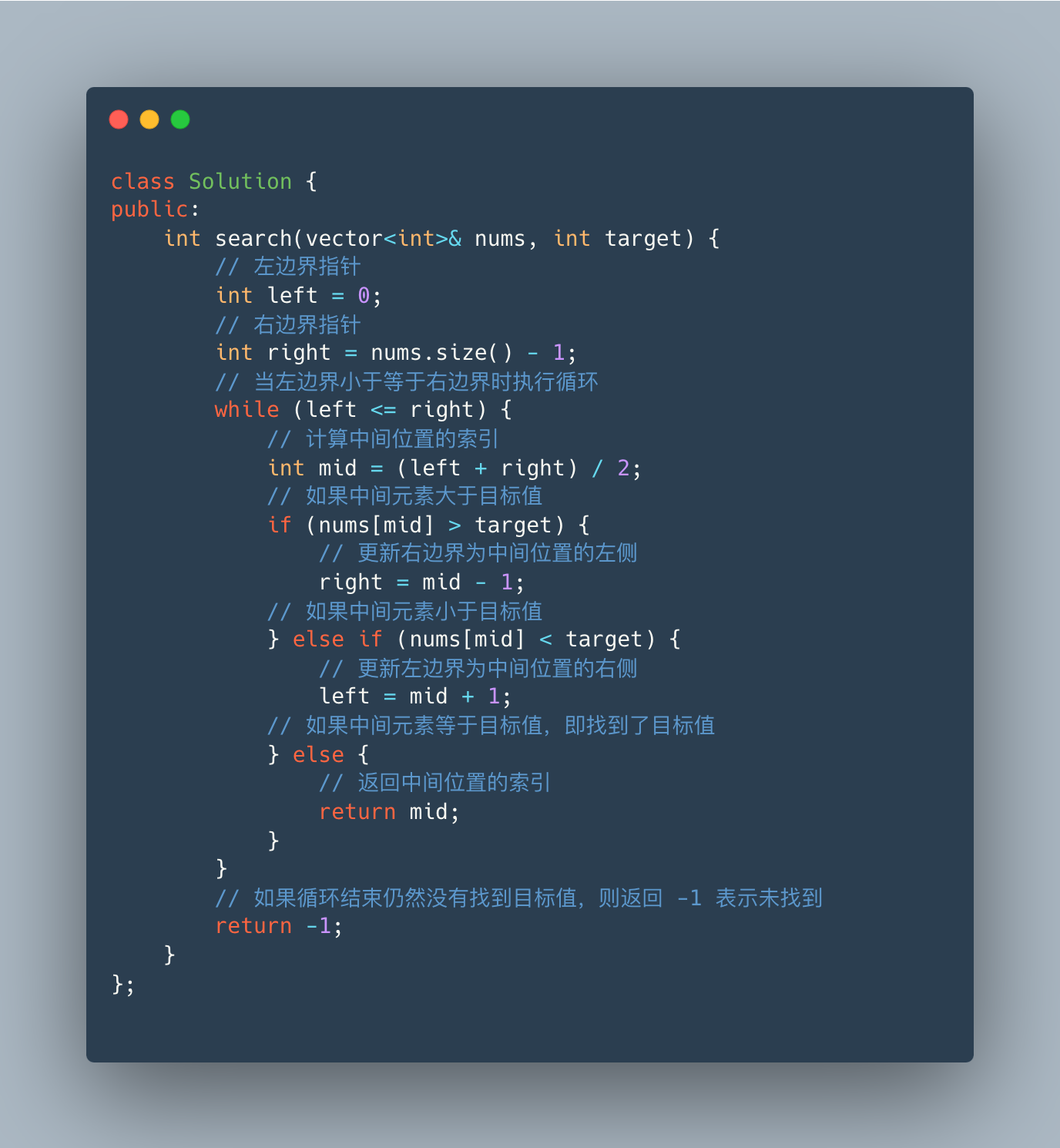
class Solution {
public:
    int search(vector<int>& nums, int target) {
        // 左边界指针
        int left = 0;  
        // 右边界指针
        int right = nums.size() - 1;  
        // 当左边界小于等于右边界时执行循环
        while (left <= right) {  
            // 计算中间位置的索引
            int mid = (left + right) / 2;  
            // 如果中间元素大于目标值
            if (nums[mid] > target) {  
                // 更新右边界为中间位置的左侧
                right = mid - 1;  
            // 如果中间元素小于目标值
            } else if (nums[mid] < target) {  
                // 更新左边界为中间位置的右侧
                left = mid + 1;  
            // 如果中间元素等于目标值，即找到了目标值
            } else {  
                // 返回中间位置的索引
                return mid; 
            }
        }
        // 如果循环结束仍然没有找到目标值，则返回 -1 表示未找到
        return -1;  
    }
};