Leetcode 18. 四数之和(画图分析)
题意:给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例: 给定数组 nums = [1, 0, -1, 0, -2, 2],和 target = 0。 满足要求的四元组集合为: [ [-1, 0, 0, 1], [-2, -1, 1, 2], [-2, 0, 0, 2] ]
解题思路:
对数组进行排序,使用四个指针 i、j 、left 和 right 分别代表要找的四个数。
排序的主要目的是为了便于使用双指针法,并且在一定程度上减少时间复杂度。
- 便于使用双指针法:在四数之和问题中,排序后可以让我们固定两个数(外层两个循环),然后使用双指针法查找剩余的两个数,使得时间复杂度从 O(N³) 降到 O(N²)(双指针法在排好序的数组中效率更高)。
- 去重:排序后,可以方便地跳过相同的元素来去重。
- 剪枝:排序后,如果固定的前两个数的和已经大于目标值
target,我们就可以提前停止搜索,避免不必要的计算。
接着我们通过枚举 i 确定第一个数,枚举 j 确定第二个数,另外两个指针 left 和 right 分别从左边 j + 1 和右边 n - 1 往中间移动,找到满足 nums[i] + nums[j] + nums[left] + nums[right] == target 的所有组合。
更加详细的可以看我下面画的图。
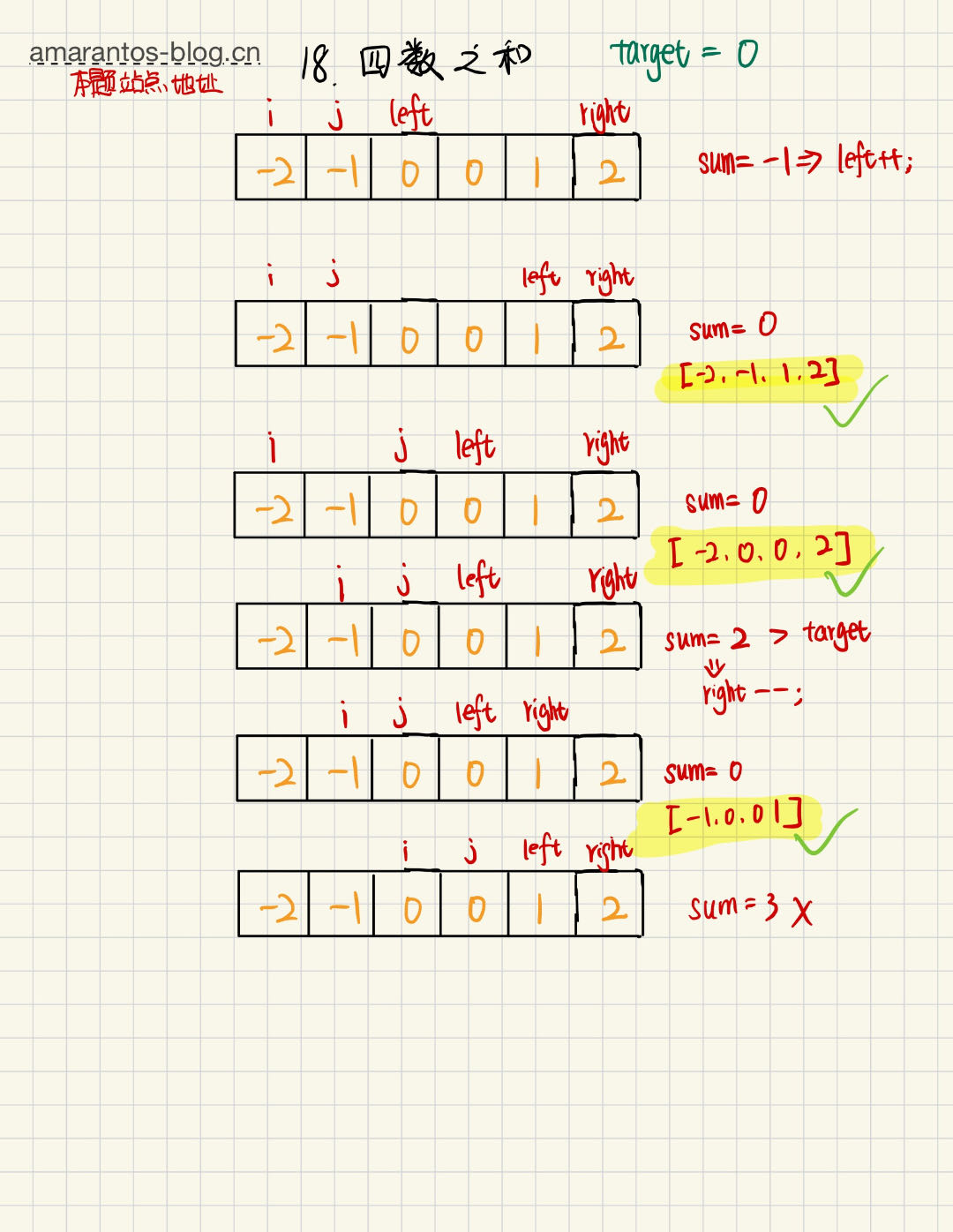
left 和 right 指针的移动逻辑,分情况讨论 sum = nums[i] + nums[j] + nums[left] + nums[right] :
sum >target:right 左移,使sum 变小
sum <target:left 右移,使sum 变大
sum =target:将组合加入结果集,left 右移继续进行检查
题目要求不能包含重复元素,所以我们要对 i、j 和 left 进行去重,去重逻辑是对于相同的数,只使用第一个。
下面的图根据nums = [1, 0, -1, 0, -2, 2],和 target = 0,来进行的步骤分析
sum = nums[i] + nums[j] + nums[left] + nums[right]
代码实现:
Java
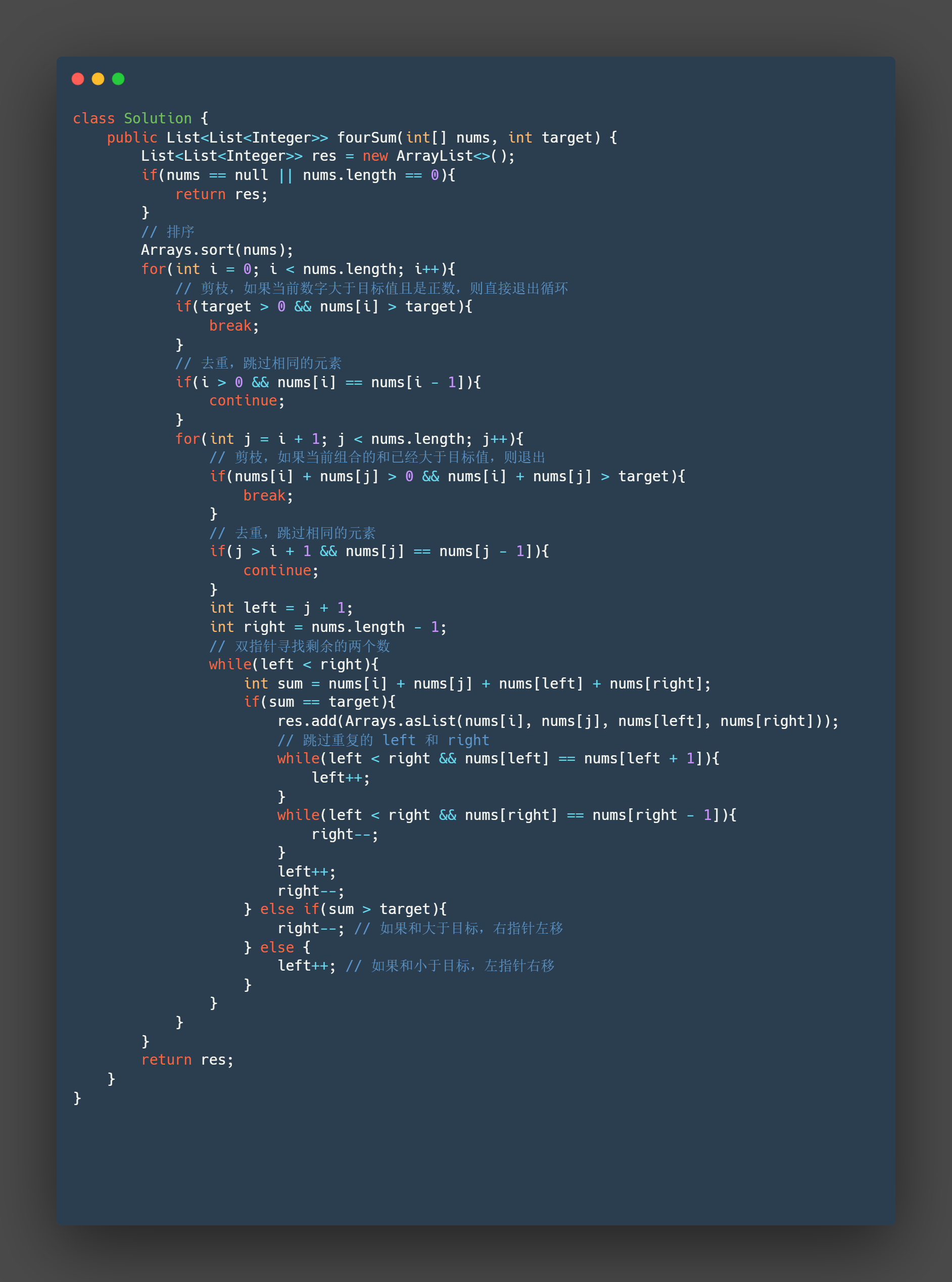
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> res = new ArrayList<>();
if(nums == null || nums.length == 0){
return res;
}
// 排序
Arrays.sort(nums);
for(int i = 0; i < nums.length; i++){
// 剪枝,如果当前数字大于目标值且是正数,则直接退出循环
if(target > 0 && nums[i] > target){
break;
}
// 去重,跳过相同的元素
if(i > 0 && nums[i] == nums[i - 1]){
continue;
}
for(int j = i + 1; j < nums.length; j++){
// 剪枝,如果当前组合的和已经大于目标值,则退出
if(nums[i] + nums[j] > 0 && nums[i] + nums[j] > target){
break;
}
// 去重,跳过相同的元素
if(j > i + 1 && nums[j] == nums[j - 1]){
continue;
}
int left = j + 1;
int right = nums.length - 1;
// 双指针寻找剩余的两个数
while(left < right){
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if(sum == target){
res.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
// 跳过重复的 left 和 right
while(left < right && nums[left] == nums[left + 1]){
left++;
}
while(left < right && nums[right] == nums[right - 1]){
right--;
}
left++;
right--;
} else if(sum > target){
right--; // 如果和大于目标,右指针左移
} else {
left++; // 如果和小于目标,左指针右移
}
}
}
}
return res;
}
}
python3

class Solution:
def fourSum(self, nums, target):
res = []
if not nums:
return res
nums.sort() # 排序
for i in range(len(nums)):
# 剪枝,如果当前数字大于目标值且是正数,直接退出循环
if target > 0 and nums[i] > target:
break
# 去重,跳过相同的元素
if i > 0 and nums[i] == nums[i - 1]:
continue
for j in range(i + 1, len(nums)):
# 剪枝,如果当前组合的和已经大于目标值,退出
if nums[i] + nums[j] > 0 and nums[i] + nums[j] > target:
break
# 去重,跳过相同的元素
if j > i + 1 and nums[j] == nums[j - 1]:
continue
left, right = j + 1, len(nums) - 1
# 双指针寻找剩余的两个数
while left < right:
sum_val = nums[i] + nums[j] + nums[left] + nums[right]
if sum_val == target:
res.append([nums[i], nums[j], nums[left], nums[right]])
# 跳过重复的 left 和 right
while left < right and nums[left] == nums[left + 1]:
left += 1
while left < right and nums[right] == nums[right - 1]:
right -= 1
left += 1
right -= 1
elif sum_val > target:
right -= 1 # 如果和大于目标,右指针左移
else:
left += 1 # 如果和小于目标,左指针右移
return res
c++
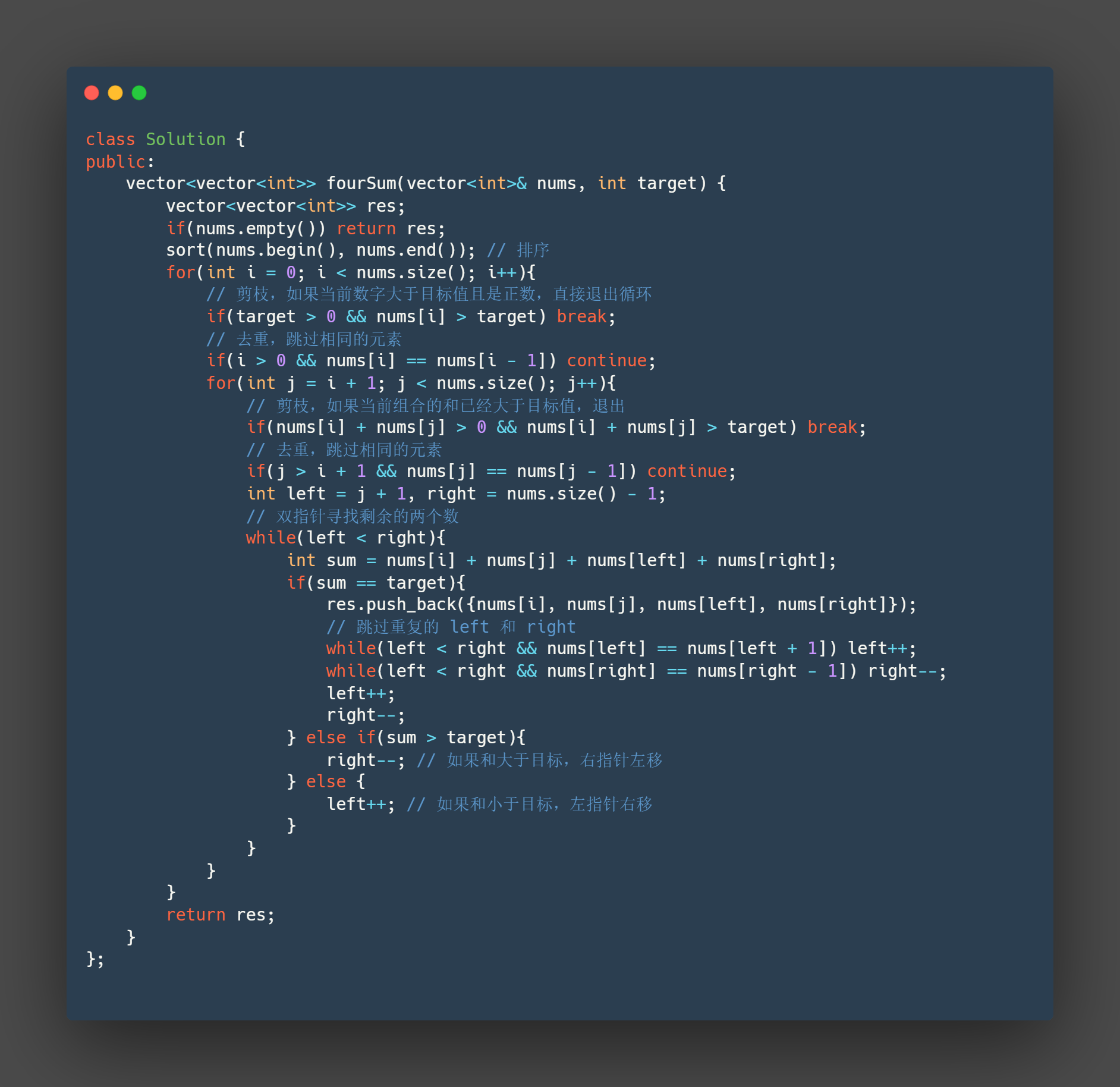
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> res;
if(nums.empty()) return res;
sort(nums.begin(), nums.end()); // 排序
for(int i = 0; i < nums.size(); i++){
// 剪枝,如果当前数字大于目标值且是正数,直接退出循环
if(target > 0 && nums[i] > target) break;
// 去重,跳过相同的元素
if(i > 0 && nums[i] == nums[i - 1]) continue;
for(int j = i + 1; j < nums.size(); j++){
// 剪枝,如果当前组合的和已经大于目标值,退出
if(nums[i] + nums[j] > 0 && nums[i] + nums[j] > target) break;
// 去重,跳过相同的元素
if(j > i + 1 && nums[j] == nums[j - 1]) continue;
int left = j + 1, right = nums.size() - 1;
// 双指针寻找剩余的两个数
while(left < right){
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if(sum == target){
res.push_back({nums[i], nums[j], nums[left], nums[right]});
// 跳过重复的 left 和 right
while(left < right && nums[left] == nums[left + 1]) left++;
while(left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
} else if(sum > target){
right--; // 如果和大于目标,右指针左移
} else {
left++; // 如果和小于目标,左指针右移
}
}
}
}
return res;
}
};
- 空间复杂度:O(N + K),其中 N 是数组长度,K 是结果集的大小。
- 时间复杂度:O(N³),排序是 O(N log N),双指针部分是 O(N³)。




评论区