LeetCode 376. 摆动序列

力扣传送门(opens new window)

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:

• 输入: [1,7,4,9,2,5]
• 输出: 6
• 解释: 整个序列均为摆动序列。

示例 2:

• 输入: [1,17,5,10,13,15,10,5,16,8]
• 输出: 7
• 解释: 这个序列包含几个长度为 7 摆动序列，其中一个可为[1,17,10,13,10,16,8]。

示例 3:

• 输入: [1,2,3,4,5,6,7,8,9]
• 输出: 2

解题思路：

这道题可以使用贪心算法来解决。我们可以通过观察摆动序列的性质，找到一种贪心策略来选择最长的摆动子序列。

思路如下：

1. 初始化两个变量：up 和 down，表示当前最后两个元素构成的子序列的最后一个差值是正数还是负数。
2. 初始化结果变量 maxLength 为 1，表示最长摆动子序列的长度，初始值为 1，因为至少会包含第一个元素。
3. 从第二个元素开始遍历整个序列。
4. 如果当前元素与前一个元素形成的差值大于零且 up 不为真，则将 up 设置为真，表示差值为正数。更新 maxLength 为当前长度加 1。
5. 如果当前元素与前一个元素形成的差值小于零且 down 不为真，则将 down 设置为真，表示差值为负数。更新 maxLength 为当前长度加 1。
6. 如果当前元素与前一个元素形成的差值不满足上述两个条件，则继续遍历下一个元素。
7. 最后返回 maxLength，即为最长摆动子序列的长度。

这种贪心策略的思路是，我们只关心序列中差值的正负交替性，而不关心具体的差值数值。只要满足正负交替的条件，我们就可以不断延长子序列的长度。

代码实现：

class Solution {
    public int wiggleMaxLength(int[] nums) {
         if (nums.length < 2) {
        return nums.length;
    }
  
    int maxLength = 1;  // 最长摆动子序列的长度
    boolean up = false;     // 差值为正数
    boolean down = false;   // 差值为负数
  
    for (int i = 1; i < nums.length; i++) {
        if (nums[i] > nums[i - 1] && !up) {
            up = true;
            down = false;
            maxLength++;
        } else if (nums[i] < nums[i - 1] && !down) {
            down = true;
            up = false;
            maxLength++;
        }
    }
  
    return maxLength;
    }
}

代码跟踪：

当我们使用示例输入 [1, 7, 4, 9, 2, 5] ，来看一下每一步变量的变化

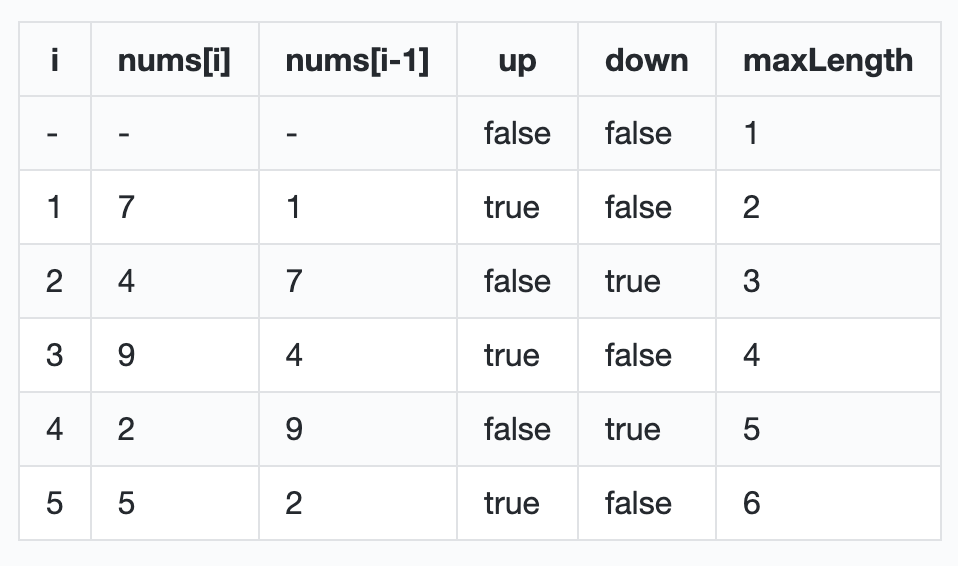
我们可以看到在每一步中变量的值和状态的变化。

最终，maxLength 的值为 6，就是我们要的最终答案。