Leetcode 452. 用最少数量的箭引爆气球

力扣传送门(opens new window)

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：

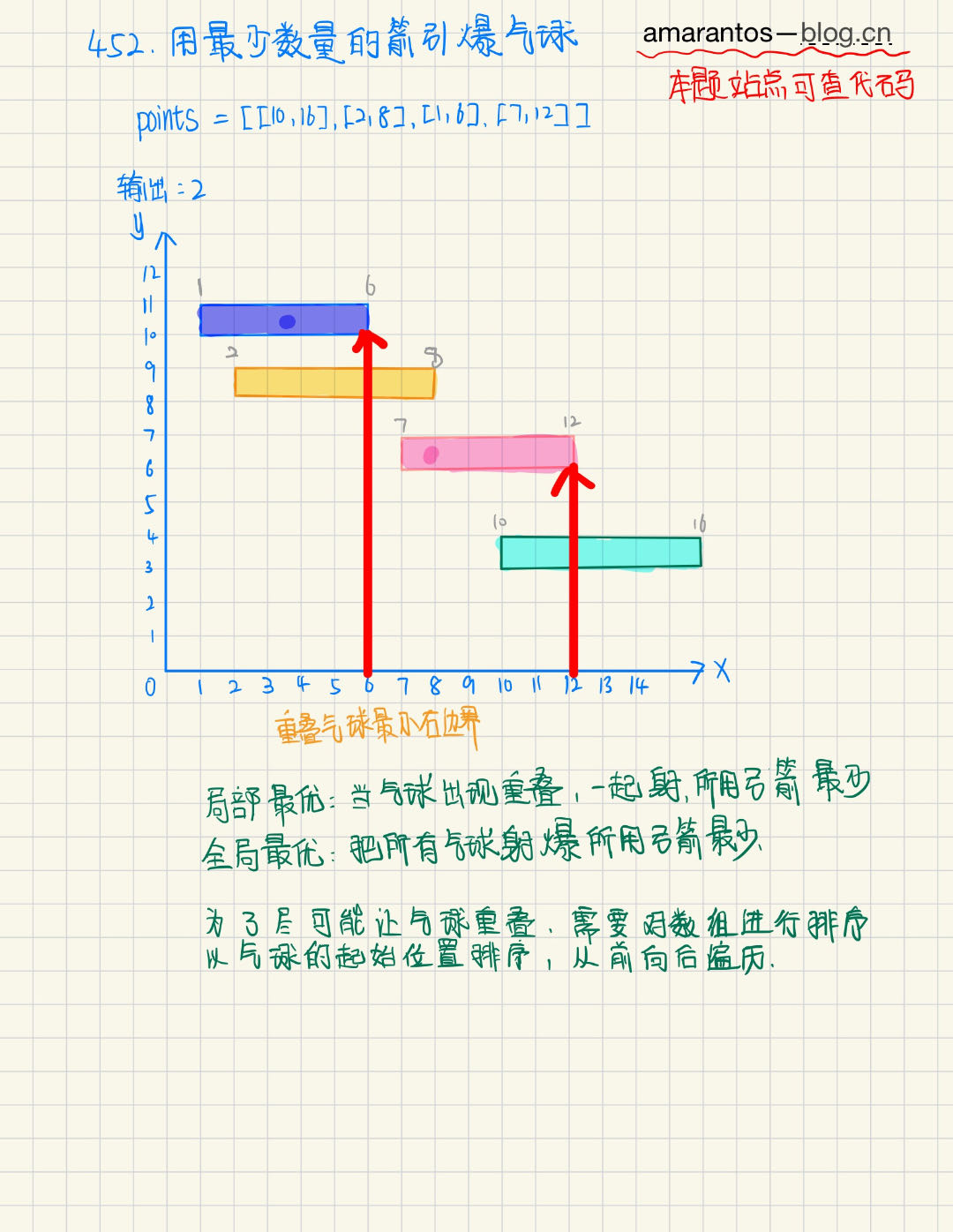
• 输入：points = [[10,16],[2,8],[1,6],[7,12]]
• 输出：2
• 解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：

• 输入：points = [[1,2],[3,4],[5,6],[7,8]]
• 输出：4

示例 3：

• 输入：points = [[1,2],[2,3],[3,4],[4,5]]
• 输出：2

示例 4：

• 输入：points = [[1,2]]
• 输出：1

示例 5：

• 输入：points = [[2,3],[2,3]]
• 输出：1

提示：

• 0 <= points.length <= 10^4
• points[i].length == 2
• -2^31 <= xstart < xend <= 2^31 - 1

解题思路：

有多少同学刚开始没读懂题目（反正我是没读懂）可以先看下面的图！！

其实就是从x轴开始向气球射击，我这里把气球画成长方形易于理解，我们可以看到每个气球之间有的有重叠部分，有的没有重叠部分，这道题目就是说如何用最少的箭来击穿所有的气球。那按照正常思路当然就是找到重叠的部分一箭击穿咯。关键就是如何找到重叠的部分。

我们还是使用贪心算法。以下是解题思路：

1. 首先，根据气球的水平直径的起始坐标对气球进行排序。这将帮助我们按顺序处理气球，从左到右扫描墙面上的气球。
2. 初始化一个变量 result为1，表示至少需要一支箭来引爆第一个气球。
3. 从第二个气球开始，遍历每个气球，检查当前气球的起始坐标是否大于前一个气球的结束坐标。如果是，表示当前气球和前一个气球没有重叠，需要额外的箭来引爆当前气球。此时，将 result增加1。
4. 如果当前气球的起始坐标小于或等于前一个气球的结束坐标，说明两个气球有重叠部分。在这种情况下，我们可以通过将当前气球的结束坐标更新为当前气球和前一个气球的结束坐标的较小值，来确保在引爆当前气球时，箭的范围尽可能地覆盖前一个气球。这样可以避免使用额外的箭。
5. 继续遍历下一个气球，重复步骤3和步骤4，直到处理完所有的气球。
6. 返回 result作为所需的最小弓箭数。

通过这种贪心算法的思路，我们可以找到一种最优的策略，尽可能少地使用弓箭，同时确保引爆所有的气球。

代码实现：

class Solution {
    public int findMinArrowShots(int[][] points) {
        if(points == null || points.length == 0){
            return 0;
        }
        //先按照start的大小进行排序
        // Arrays.sort(points,(o1,o2)->(o1[0] - o2[0]));使用这个判断方式会溢出
    
        //排序的方式是使用一个比较器(a, b) -> Integer.compare(a[0], b[0])，它比较每个数组内的第一个元素（即[0]索引处的值）。
        //这将使得points数组按照子数组的第一个元素（即气球的起始位置）的升序进行排序。
        Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));
        int result = 1;
        for(int i = 1;i < points.length;i++){
            //检查当前气球的起始位置是否大于前一个气球的结束位置。
            //如果是，说明当前气球和前一个气球不重叠，需要额外的箭来引爆当前气球，因此result增加1
            if(points[i][0] > points[i-1][1]){
                result++;
                //如果当前气球的起始位置小于或等于前一个气球的结束位置，则说明两个气球有重叠部分。
                //在这种情况下，我们需要尽可能地减少使用的箭数。
                //通过将当前气球的结束位置更新为当前气球和前一个气球的结束位置的较小值，可以确保在引爆当前气球时，箭的范围尽可能地覆盖前一个气球。
            }else{
                points[i][1] = Math.min(points[i][1],points[i-1][1]);
            }
        }
        //最后，返回result作为所需的最小箭数
        return result;
    }
}

觉得有用的点个赞再走吧~