Leetcode 239. 滑动窗口最大值(画图分析)
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1 输出:[1]
提示:
1 <= nums.length <= 10<sup>5</sup>-10<sup>4</sup> <= nums[i] <= 10<sup>4</sup>1 <= k <= nums.length
解题思路:
我们可以自定义一个队列,当我们放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,这个自定义的队列就可以告诉我们里面的最大值是什么。
这个队列应该长这个样子:
class MyQueue {
public void poll(int val) {
}
public void add(int val) {
}
public int peek() {
}
}
这个队列的核心就是:
poll(int val): 该方法用于移除队列中指定的值。在滑动窗口的情况下,当窗口滑动时,最左侧的元素会被移除。如果队列不为空且队首元素等于指定值,那么它会被移除。add(int val): 该方法用于将元素添加到队列中,并维护队列的单调性。在滑动窗口的情况下,每当新的元素进入窗口时,我们需要保持队列的单调性(即,队列中的元素应该按照降序排列)。具体操作是,**如果队列不为空且新元素大于队尾元素,那么连续移除队尾元素,直到队列为空或者新元素小于等于队尾元素。**然后,将新元素添加到队尾,以保持队列的单调性。peek(): 该方法用于返回队首元素,即当前窗口的最大值。在滑动窗口的情况下,队首元素始终代表当前窗口的最大值。
下面是画图理解:
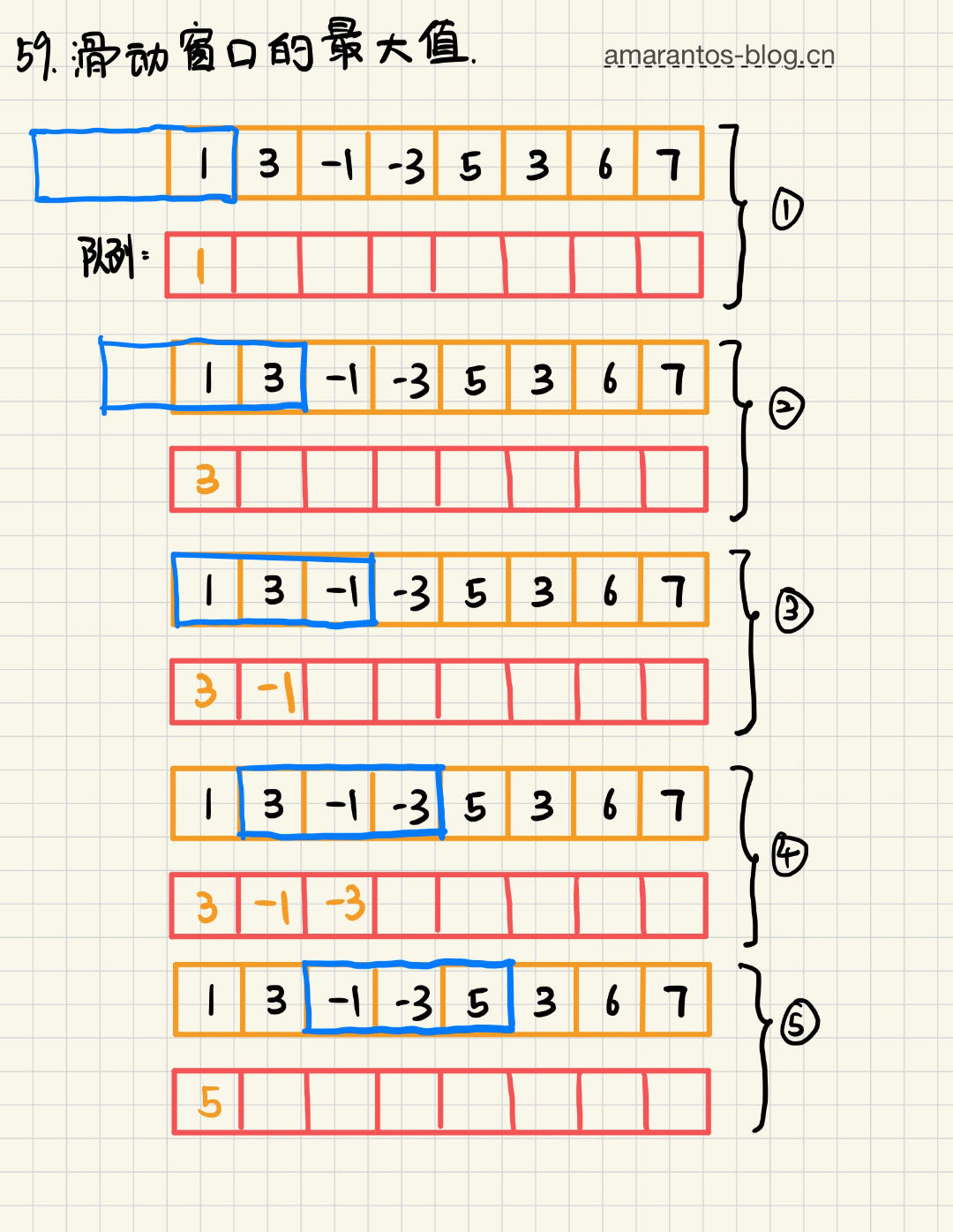
基于刚刚说过的单调队列的规则,代码不难实现
代码实现:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0 || nums.length == 1) {
return nums;
}
// 结果数组的长度
int len = nums.length - k + 1;
// 结果数组
int[] res = new int[len];
// 结果数组的索引
int num = 0;
// 自定义队列对象
MyQueue myQueue = new MyQueue();
for (int i = 0; i < k; i++) {
// 初始化队列,将前k个元素加入队列
myQueue.add(nums[i]);
}
// 存储当前窗口的最大值到结果数组中
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
// 移除窗口最左侧的元素
myQueue.poll(nums[i - k]);
// 添加新元素到队列
myQueue.add(nums[i]);
// 存储当前窗口的最大值到结果数组中
res[num++] = myQueue.peek();
}
// 返回结果数组
return res;
}
}
class MyQueue {
// 使用双端队列实现
Deque<Integer> deque = new LinkedList();
public void poll(int val) {
// 如果队首元素等于指定值
if (!deque.isEmpty() && deque.peek() == val) {
// 移除队首元素
deque.poll();
}
}
public void add(int val) {
// 如果队列不为空且val大于队尾元素
while (!deque.isEmpty() && val > deque.getLast()) {
// 连续移除队尾元素,直到队列为空或者val小于等于队尾元素
deque.removeLast();
}
// 将val加入队尾
deque.add(val);
}
public int peek() {
// 返回队首元素,即当前窗口的最大值
return deque.peek();
}
}
通过使用 MyQueue,我们可以在滑动窗口每次滑动时,高效地获取当前窗口的最大值。它的实现保证了时间复杂度为O(n),其中n是数组的长度,因为每个元素最多进出队列一次。这样,我们可以有效地解决滑动窗口最大值的问题。




评论区