Leetcode 541. 反转字符串II(画图分析)
给定一个字符串 s 和一个整数 k,从字符串开头算起, 每计数至 2k 个字符,就反转这 2k 个字符中的前 k 个字符。
如果剩余字符少于 k 个,则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
示例:
输入: s = "abcdefg", k = 2
输出: "bacdfeg"
解题思路:
我们先看题目,这道题说的是,每隔2k个字符,反转前k个字符,剩下的不足k个字符的,将剩余字符全部反转,小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
前面每隔2k个字符,反转前k个字符还好处理,主要是我们如何处理最后的几个字符呢?
还是准备两个指针 left 和 right ,首先我们for循环遍历整个字符串,i 初始值为0,让 i 每次跳跃 2*k 个字符,并且 left 被赋值为 i,right这里赋值为多少合适呢?我们仔细思考一下
我们简单计算下right = left+k-1;
left 是当前需要翻转的子字符串的起始位置,而 right 是我们想要翻转的子字符串的结束位置。通常情况下,right 应该等于 left + k - 1,即从 left 开始往右数 k 个字符。但是如果字符串的长度不足以支持完整的 k 个字符时,left + k - 1 可能会超出字符串的实际长度。
因此:
- left + k - 1:是理论上希望的右边界,即从 left 开始数
k个字符后的右边界。 - ch.length - 1:是字符串的最后一个字符的索引,这是数组允许的最大索引。
为了确保 right 不超出字符数组的范围,使用 Math.min() 来选择实际的右边界:
int right = Math.min(ch.length - 1, left + k - 1);
这行代码的含义是:
- 如果 left + k - 1 小于 ch.length - 1,说明还有足够的字符去反转 k 个字符,right 就等于 left + k - 1。
- 如果 left + k - 1 大于 ch.length - 1,说明剩下的字符不足
k个,此时 right 取值为 ch.length - 1,即字符串的最后一个字符。
举例说明:
- 正常情况:
- 输入字符串:s = "abcdefg",k = 2
- 初始时:left = 0
- 计算 left + k - 1 = 0 + 2 - 1 = 1
- ch.length - 1 = 6
- 因此,right = Math.min(6, 1) = 1,正确翻转第 0 到 1 位置的字符。
- 字符串长度不足
k个字符:- 输入字符串:s = "abc",k = 2
- 初始时:left = 0
- 计算 left + k - 1 = 0 + 2 - 1 = 1
- ch.length - 1 = 2
- 因此,right = Math.min(2, 1) = 1,正常翻转第 0 到 1 位置的字符。
- 剩余字符不足
k个:- 输入字符串:s = "abc",k = 5
- 初始时:left = 0
- 计算 left + k - 1 = 0 + 5 - 1 = 4,超出了字符串的长度
- ch.length - 1 = 2
- 因此,right = Math.min(2, 4) = 2,翻转第 0 到 2 位置的字符,即翻转所有剩余字符。
总结
Math.min(ch.length - 1, left + k - 1) 的作用是确保右边界 right 不会超过字符串的实际长度,从而避免数组越界问题。
理解了上面的这道题目的关键,下面我们看图来理解这道题。

代码实现:
java
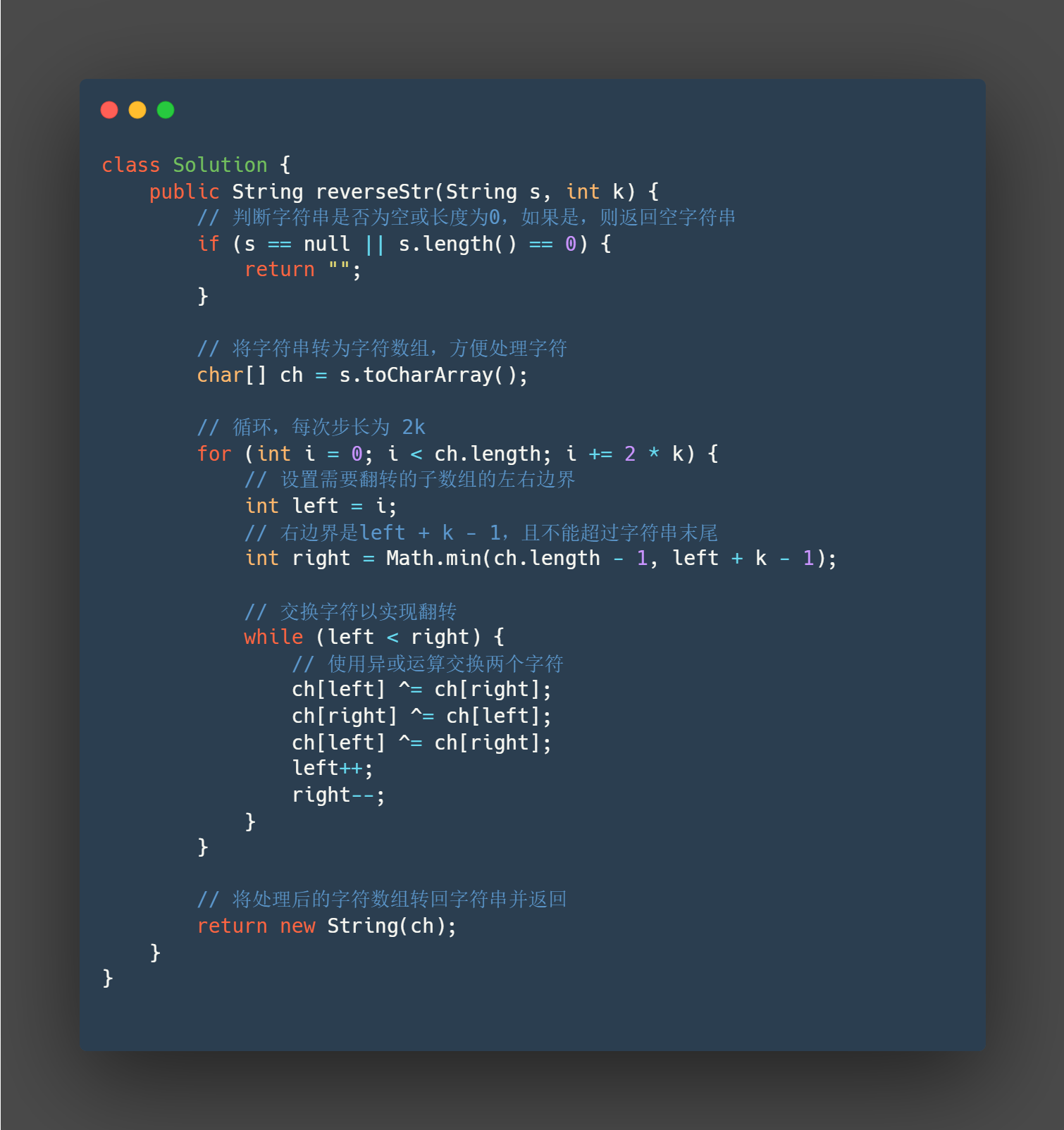
class Solution {
public String reverseStr(String s, int k) {
// 判断字符串是否为空或长度为0,如果是,则返回空字符串
if (s == null || s.length() == 0) {
return "";
}
// 将字符串转为字符数组,方便处理字符
char[] ch = s.toCharArray();
// 循环,每次步长为 2k
for (int i = 0; i < ch.length; i += 2 * k) {
// 设置需要翻转的子数组的左右边界
int left = i;
// 右边界是left + k - 1,且不能超过字符串末尾
int right = Math.min(ch.length - 1, left + k - 1);
// 交换字符以实现翻转
while (left < right) {
// 使用异或运算交换两个字符
ch[left] ^= ch[right];
ch[right] ^= ch[left];
ch[left] ^= ch[right];
left++;
right--;
}
}
// 将处理后的字符数组转回字符串并返回
return new String(ch);
}
}
代码分析:
我们直接按题意进行模拟:反转每个下标从 2k 的倍数开始的,长度为 k的子串。若该子串长度不足 k,则反转整个子串。在代码中,right 的计算是为了确定需要翻转的子串的结束索引。这里使用了 Math.min(ch.length - 1, left + k - 1) 的原因是确保 right 的值不会超过数组的最大索引。
让我们来解释一下为什么要这样写:
ch.length是数组ch的长度,即数组中元素的个数。left + k - 1表示子串的结束索引。left是子串的起始索引,k是子串的长度,所以left + k - 1是子串的结束索引。Math.min(ch.length - 1, left + k - 1)会返回ch.length - 1和left + k - 1中较小的值。这是为了确保right不会超过数组的最大索引。
例如,假设数组 ch 的长度为 10,并且当前的 left 是 3,k 是 5。根据上述代码,我们有:
left + k - 1的值为3 + 5 - 1 = 7,即子串的结束索引为7。ch.length - 1的值为10 - 1 = 9,即数组的最大索引为9。- 因为
7小于等于9,所以right的值将为7,这是符合要求的子串结束索引。
通过这种写法,可以确保在翻转子串时不会超出数组的边界,避免出现索引越界的错误。
异或算法:
- 如果两个二进制位相同(都是0或都是1),则异或的结果为0。
- 如果两个二进制位不同(一个是0,另一个是1),则异或的结果为1。
A B A XOR B
0 0 0
0 1 1
1 0 1
1 1 0
当代码执行 ch[left] ^= ch[right] 时,它使用异或(XOR)运算符对数组中的两个元素进行交换,而无需使用额外的变量。这种交换方式是通过异或的性质实现的。
以下是一个例子来说明这个过程:
假设我们有一个数组 ch,其内容为 ['a', 'b']。现在,我们希望交换数组中的这两个元素。
初始状态下,ch[left] 是 'a',而 ch[right] 是 'b'。
执行 ch[left] ^= ch[right],相当于执行 ch[left] = ch[left] ^ ch[right]。
- 在二进制表示中,
'a'对应的 ASCII 值是0b01100001,'b'对应的 ASCII 值是0b01100010。 - 执行
0b01100001 ^ 0b01100010,得到结果0b00000011,即 ASCII 值为3的字符(即 ETX,表示文本结束)。
接下来,执行 ch[right] ^= ch[left],相当于执行 ch[right] = ch[right] ^ ch[left]。
- 在二进制表示中,
'b'对应的 ASCII 值是0b01100010,而ch[left]的值为3(即0b00000011)。 - 执行
0b01100010 ^ 0b00000011,得到结果0b01100001,即 ASCII 值为97的字符'a'。
最后,执行 ch[left] ^= ch[right],相当于执行 ch[left] = ch[left] ^ ch[right]。
- 在这一步中,
ch[left]的值为3(即0b00000011),而ch[right]的值为'a'对应的 ASCII 值97(即0b01100001)。 - 执行
0b00000011 ^ 0b01100001,得到结果0b01100010,即 ASCII 值为98的字符'b'。
最终,数组 ch 的状态变为 ['b', 'a'],成功地完成了两个元素的交换。
这种通过异或运算实现的交换方式可以应用于其他数据类型,不仅限于字符。它是一种常见的技巧,用于在不使用额外变量的情况下交换两个值。
python3

class Solution:
def reverseStr(self, s: str, k: int) -> str:
# 如果字符串为空或长度为0,直接返回空字符串
if not s:
return ""
# 将字符串转换为字符列表(类似于Java的字符数组)
ch = list(s)
# 循环,步长为2k
for i in range(0, len(ch), 2 * k):
# 计算左边界和右边界,右边界不能超过末尾
left = i
right = min(len(ch) - 1, left + k - 1)
# 翻转字符
while left < right:
# 直接交换两个字符
ch[left], ch[right] = ch[right], ch[left]
left += 1
right -= 1
# 返回翻转后的字符串
return ''.join(ch)
c++

class Solution {
public:
string reverseStr(string s, int k) {
// 如果字符串为空或长度为0,直接返回空字符串
if (s.empty()) {
return "";
}
// 遍历字符数组,步长为2k
for (int i = 0; i < s.size(); i += 2 * k) {
// 计算左边界和右边界,右边界不能超过字符串末尾
int left = i;
int right = min((int)s.size() - 1, left + k - 1);
// 翻转字符
while (left < right) {
// 使用标准交换函数交换两个字符
swap(s[left], s[right]);
left++;
right--;
}
}
// 返回处理后的字符串
return s;
}
};
时间复杂度分析:
代码的核心逻辑是反转字符串中每隔 2k 个字符的前 k 个字符。接下来,我们对这部分的时间复杂度进行分析:
- 遍历字符串:
- 我们使用了一个 for 循环,其中步长为 2 * k。在每次循环中,我们从 i = 0 开始,每次跳跃 2 * k 个字符,直到遍历完字符串。也就是说,总共需要遍历整个字符串的长度 n。
- 因此,循环次数约为 n / (2 * k)。
- 每次反转 k 个字符:
- 在每次循环中,我们要反转前 k 个字符(或者少于 k 个字符,如果剩余字符不足)。
- 反转 k 个字符的时间复杂度为 O(k),因为交换操作需要遍历 k/2 次,但可以视为常数时间内的线性操作。
综上,我们可以得到:
- 总循环次数:n / (2 * k)
- 每次反转的操作时间:O(k)
因此,总时间复杂度为:
O(n/2k×k)
空间复杂度分析:
- 额外空间:
- 我们使用了一个字符数组 ch 来存储字符串的字符。在最坏情况下,这个字符数组的大小与字符串长度 n 相等。因此,所需的额外空间是 O(n)。
- 除此之外,代码中使用的变量(如 left 和 right)是常数空间,和输入字符串的长度无关。
因此,额外的空间复杂度为 O(n)。
综上,时间复杂度和空间复杂度如下:
- **时间复杂度:**O(n),其中 n 是字符串的长度。
- **空间复杂度:**O(n),用于存储字符数组。




评论区